
【题目】如图1,在正方形ABCD(正方形四边相等,四个角均为直角)中,AB=8,P为线段BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交AD于点N.
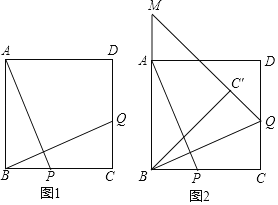
(1)求证:BP=CQ;
(2)若BP=![]() PC,求AN的长;
PC,求AN的长;
(3)如图2,延长QN交BA的延长线于点M,若BP=x(0<x<8),△BMC'的面积为S,求S与x之间的函数关系式.
【答案】(1)见解析;(2)4.8;(3)![]()
【解析】
(1)证明△ABP≌△BCQ即可得到结论;
(2)证明Rt△ABN≌△Rt△C'BN求出DQ,设AN=NC'=a,则DN=8﹣a,利用勾股定理即可求出a;
(3)过Q点作QG⊥BM于G,设MQ=BM=y,则MG=y﹣x,利用勾股定理求出MQ,再根据面积相减得到答案.
解:(1)证明:∵∠ABC=90°
∴∠BAP+∠APB=90°
∵BQ⊥AP
∴∠APB+∠QBC=90°,
∴∠QBC=∠BAP,
在△ABP于△BCQ中,
 ,
,
∴△ABP≌△BCQ(ASA),
∴BP=CQ,
(2)由翻折可知,AB=BC',
连接BN,在Rt△ABN和Rt△C'BN中,AB=BC',BN=BN,

∴Rt△ABN≌△Rt△C'BN(HL),
∴AN=NC',
∵BP=![]() PC,AB=8,
PC,AB=8,
∴BP=2=CQ,CP=DQ=6,
设AN=NC'=a,则DN=8﹣a,
∴在Rt△NDQ中,(8﹣a)2+62=(a+2)2
解得:a=4.8,
即AN=4.8.
(3)解:过Q点作QG⊥BM于G,由(1)知BP=CQ=BG=x,BM=MQ.

设MQ=BM=y,则MG=y﹣x,
∴在Rt△MQG中,y2=82+(y﹣x)2,
∴![]() .
.
∴S△BMC′=S△BMQ﹣S△BC'Q=![]() ,
,
=![]() ,
,
=![]() .
.


科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
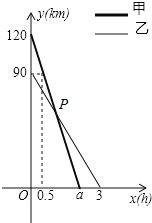
【题目】在一条笔直的公路旁依次有![]() 三个村庄,甲、乙两人同时分别从
三个村庄,甲、乙两人同时分别从![]() 两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向
两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向![]() 村,最终到达
村,最终到达![]() 村,设甲、乙两人到
村,设甲、乙两人到![]() 村的距离
村的距离![]() ,
,![]() (
(![]() )与行驶时间
)与行驶时间![]() (
(![]() )之间的函数关系如图所示,请解答下列问题:
)之间的函数关系如图所示,请解答下列问题:
(1)![]() 两村间的距离为
两村间的距离为 ![]() ;
;
(2)求![]() 的关系式,并写出自变量
的关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)求出图中点![]() 的坐标,并解释该点坐标所表示的实际意义.
的坐标,并解释该点坐标所表示的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.
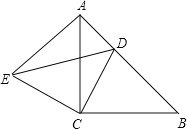
(1)求证:AE=BD;
(2)试探究线段AD、BD与CD之间的数量关系;
(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:2![]() ,CD=
,CD=![]() ,求线段AB的长.
,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.
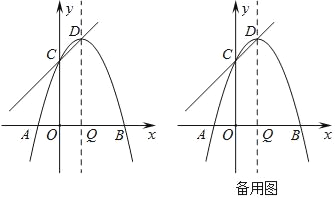
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
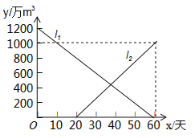
【题目】今年夏天,重庆各区持续高温日数达到历史之最,受持续高温和连日无雨的影响,重庆某水库的蓄水量随时间的增加而减少,己知原有蓄水量![]() (万
(万![]() )与干旱持续时间
)与干旱持续时间![]() (天)的关系如图中线段
(天)的关系如图中线段![]() 所示,针对这种干旱情况,从第20天开始向水库注水,注水量
所示,针对这种干旱情况,从第20天开始向水库注水,注水量![]() (万
(万![]() )与时间
)与时间![]() (天)的关系如图中线段
(天)的关系如图中线段![]() 所示(不考虑其他因素).若总蓄水量不多于900万
所示(不考虑其他因素).若总蓄水量不多于900万![]() 为严重干早,则该水库发生严重干旱共__________天
为严重干早,则该水库发生严重干旱共__________天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作线段
作线段![]() 且
且![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)点![]() 的坐标轴__________,点
的坐标轴__________,点![]() 的坐标轴__________;
的坐标轴__________;
(2)直接写出点![]() 的坐标轴__________,并求出直线
的坐标轴__________,并求出直线![]() 的函数关系式;
的函数关系式;
(3)若点![]() 是图1中直线
是图1中直线![]() 上的一点,连接
上的一点,连接![]() ,得到图2,当点
,得到图2,当点![]() 在第二象限,且到
在第二象限,且到![]() 轴,
轴,![]() 轴的距离相等时,直接写出
轴的距离相等时,直接写出![]() 的面积;
的面积;
(4)若点![]() 是图1中坐标平面内不同于点
是图1中坐标平面内不同于点![]() 、点
、点![]() 的一点,当以点
的一点,当以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等时,直接写出点
全等时,直接写出点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
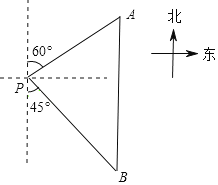
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com