
(1)已知方程x2+px+q=0(p2-4q≥0)的两根为x1、x2,求证:x1+x2=-p,x1·x2=q.(2)已知抛物线y=x2+px+q与x轴交于点A、B,且过点(―1,―1),设线段AB的长为d,当p为何值时,d2取得最小值并求出该最小值.
(1)证明见解析(2) 当p=2时,d 2的最小值是4
【解析】(1)证明:∵a=1,b=p,c=q,p2﹣4q≥0,
∴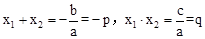 。
。
(2)解:把(﹣1,﹣1)代入y=x2+px+q得p﹣q=2,即q=p﹣2。
设抛物线y=x2+px+q与x轴交于A、B的坐标分别为(x1,0)、(x2,0)。
∵d=|x1﹣x2|,
∴d2=(x1﹣x2)2=(x1+x2)2﹣4 x1•x2=p2﹣4q=p2﹣4p+8=(p﹣2)2+4。
∴当p=2时,d 2的最小值是4。
(1)根据一元二次方程根与系数的关系可直接证得。
【教材中没有元二次方程根与系数的关系可先根据求根公式得出x1、x2的值,再求出两根的和与积即可】
(2)把点(﹣1,﹣1)代入抛物线的解析式,再由d=|x1﹣x2|可得d2关于p的函数关系式,应用二次函数的最值原理即可得出结论。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| b |
| a |
| c |
| a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com