
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
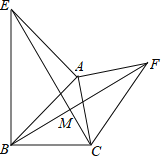
求证:(1)EC=BF;
(2)EC⊥BF;
(3)连接AM,求证:AM平分∠EMF.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)先求出∠EAC=∠BAF,然后利用“边角边”证明△ABF和△AEC全等,根据全等三角形对应边相等即可证明;
(2)根据全等三角形对应角相等可得∠AEC=∠ABF,设AB、CE相交于点D,根据∠AEC+∠ADE=90°可得∠ABF+∠ADM=90°,再根据三角形内角和定理推出∠BMD=90°,从而得证.
(3)作AP⊥CE于P,AQ⊥BF于Q.由△EAC≌△BAF,推出AP=AQ(全等三角形对应边上的高相等).由AP⊥CE于P,AQ⊥BF于Q,可得AM平分∠EMF;
证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△ABF和△AEC中,
∵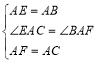 ,
,
∴△ABF≌△AEC(SAS),
∴EC=BF;
(2)根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°,
所以EC⊥BF.
(3)作AP⊥CE于P,AQ⊥BF于Q.如图:

∵△EAC≌△BAF,
∴AP=AQ(全等三角形对应边上的高相等).
∵AP⊥CE于P,AQ⊥BF于Q,
∴AM平分∠EMF.


科目:初中数学 来源: 题型:
【题目】如图,EF⊥AC于点F,DB⊥AC于点M,∠1=∠2,∠3=∠C,请问AB与MN平行吗?说明理由.完成下列推理过程:

解:AB∥MN.理由如下:
∵EF⊥AC,DB⊥AC,(已知),
∴∠CFE=∠CMD=90°,( )
∴EF∥DM,( )
∴∠2=∠CDM,( )
∵∠1=∠2,(已知),
∴∠1=∠ ( )
∴MN∥CD,( )
∵∠3=∠C,(已知),
∴AB∥CD,( ),
∴AB∥MN.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位计划在春节期间组织员工![]() 人去旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元人.两家旅行社对10人以上的团体推出了不同的优惠措施:甲旅行社对每位员工七五折优惠:乙旅行社免去一位带队员工的费用,其余员工八折优惠
人去旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元人.两家旅行社对10人以上的团体推出了不同的优惠措施:甲旅行社对每位员工七五折优惠:乙旅行社免去一位带队员工的费用,其余员工八折优惠
(1)求甲、乙两家旅行社的费用分别为多少元?(用含 ![]() 的代数式表示)
的代数式表示)
(2)若该单位组织包括带队员工在内共20名员工去旅游,你认为该单位选择哪家旅行社比较优惠?并通过计算说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣4,4),一个以A为顶点的45°角绕点A旋转,角的两边分别交x轴正半轴,y轴负半轴于E、F,连接EF.当△AEF是直角三角形时,点E的坐标是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为加快美丽乡村建设,建设秀美幸福宿州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)乙镇3个A类美丽村庄和6个B类村庄改建共需资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得线段PE,连接BE,则∠CBE等于( )
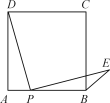
A. 75° B. 60° C. 45° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
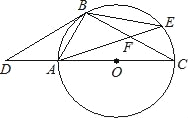
【题目】如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,弦AE与BC相交于点F,且CF=9,cos∠BFA=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com