
分析 (1)设酸味售价为每千克x元,甜味售价为每千克y元,根据题意列出方程组即可解决问题.
(2)设购买酸味n千克,总费用为m元,则购买甜味12-n千克,路程不等式求出n的范围,再构建一次函数,利用一次函数的性质解决最值问题.
解答 解:(1)设酸味售价为每千克x元,甜味售价为每千克y元,
根据题意得:$\left\{\begin{array}{l}2x+3y=90\\ x+2y=55\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=15\\ y=20\end{array}\right.$
答:酸味售价为每千克15元,甜味售价为每千克20元.
(2)设购买酸味n千克,总费用为m元,则购买甜味12-n千克,
∴12-n≥2n,
∴n≤4
∴m=15n+20(12-n)=-5n+240
∵k=-5<0∴m随n的增大而减小
∴当n=4时,m=220
答:购买酸味4千克,甜味8千克时,总费用最少.
点评 本题考查一次函数的应用、二元一次方程组等知识,解题的关键是学会设未知数,列出解方程组解决问题,学会构建一次函数,利用一次函数的性质解决最值问题,属于中考常考题型.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | a-4>b-4 | B. | -4a>-4b | C. | $\frac{a}{4}$>$\frac{b}{4}$ | D. | a+n>b+n |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{8}$-2$\sqrt{2}$=0 | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{(-5)^{2}}$=-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
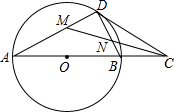 如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
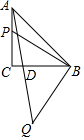 如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.
如图,△ABC是等腰直角三角形,∠C=90°,点P是直线AC上一个动点,连结BP,过点B作BQ⊥BP,且使BP=BQ,连结AQ且与直线BC相交于点D.若AP=2,AC=5,则BD的长为4或6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com