
分析 (1)根据152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,可得952=9×10×100+25,据此解答即可.
(2)根据152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,可得(a5)2=a×(a+1)×100+25,据此解答即可.
解答 解:(1)∵152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,
∴952=9×10×100+25=9025.
(2)∵152=1×2×100+25=225,252=2×3×100+25=625,352=3×4×100+25=1225,…,
∴(n5)2=n×(n+1)×100+25=100n(n+1)+25.
故答案为:9×10×100+25=9025;(n5)2=n×(n+1)×100+25=100n(n+1)+25.
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律解决问题.


科目:初中数学 来源: 题型:解答题
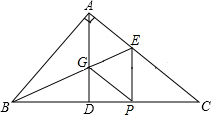 如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?
如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
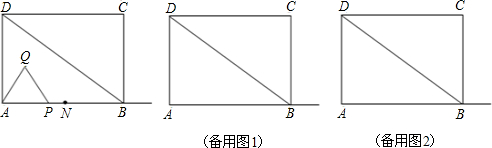
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com