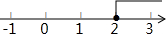Question

解不等式组，并把它们的解集在数轴上表示出来．
（1）6x≤7x-2
（2）

2x-1

3

-4＜-

x+4

2

（3）

x-3 2 +3≥x 1-3(x-1)＜8-x

（4）

2x-1＞0 1 2 (x+4)＜3

．

Answer 1

分析：（1）移项合并，然后系数化1，即可求得答案．在数轴上表示时：注意此题为实心点，方向向右．
（2）首先去分母，然后去括号，移项合并，系数化1，即可求得答案．在数轴上表示时：注意此题为空心点，方向向左．
（3）首先分别解两个一元一次不等式，然后求得其解集即可．注意在数轴上表示时：注意若边界点含于解集为实心点，不含于解集即为空心点，此题-2处为空心点，3处为实心点．
（4）首先分别解两个一元一次不等式，然后求得其解集即可．注意在数轴上表示时：注意若边界点含于解集为实心点，不含于解集即为空心点，此题均是空心点．

解答：解：（1）移项合并得：-x≤-2，
系数化1得：x≥2；
∴原不等式的解集为：x≥2；
在数轴上表示为：


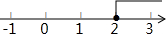
（2）去分母得：2（2x-1）-24＜-3（x+4），
去括号得：4x-2-24＜-3x-12，
移项合并得：7x＜14，
系数化1，得：x＜2；
∴原不等式的解集为：x＜2；
在数轴上表示为：


（3）∵

x-3 2 +3≥x   ① 1-3(x-1)＜8-x  ②

，
由①得：x≤3，
由②得：x＞-2，
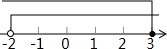
∴原不等式组的解集为：-2＜x≤3；
在数轴上表示为：


（4）∵

2x-1＞0  ① 1 2 (x+4)＜3 ②

，
由①得：x＞

1

2

，
由②得：x＜2，
∴原不等式组的解集为：

1

2

＜x＜2．
在数轴上表示为：

点评：此题考查了一元一次不等式（组）的解法．注意解不等式依据不等式的基本性质，特别是在系数化为1这一个过程中要注意不等号的方向的变化．去分母的过程中注意不能漏乘没有分母的项．用数轴表示不等式的解集时：注意时实心点还是空心点，方向是向右还是向左．