
 x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y=
x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y= x的图象的对称点为C.
x的图象的对称点为C. x的图象于点D,连结AC,交正比例函数y=
x的图象于点D,连结AC,交正比例函数y= x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.
x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.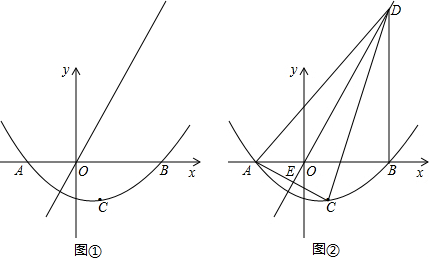
 x2+bx+c上,
x2+bx+c上, ,
, ,c=-
,c=- .
. x上,且F(2,
x上,且F(2, ).
). ,OH=2,
,OH=2, =
= ,∴∠FOB=60°.
,∴∠FOB=60°.
 x对称,∴OC=OA=2,∠COE=∠AOE=60°.
x对称,∴OC=OA=2,∠COE=∠AOE=60°. =
= ,OK=OC•cos60°=2×
,OK=OC•cos60°=2× =1.
=1. ).
). x2-
x2- x-
x- ,当x=1时,y=-
,当x=1时,y=- ,
, =
= =
= .
. ,AB=OA+OB=5.
,AB=OA+OB=5. =
= =2
=2 .
. x对称,
x对称, ,∠DAC=∠DCA,AE=CE=
,∠DAC=∠DCA,AE=CE= AC=
AC= .
.
 ,即:
,即: ,
,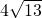 t+3=0,
t+3=0, 或t=
或t= (t>
(t> ,故舍去)
,故舍去) .
. x与x轴所夹锐角为60°,则可推出在Rt△CEK中,∠COK=60°,解此直角三角形即可求出点C的坐标;
x与x轴所夹锐角为60°,则可推出在Rt△CEK中,∠COK=60°,解此直角三角形即可求出点C的坐标;

科目:初中数学 来源: 题型:
 22、如图,已知二次函数y=(1-m)x2+4x-3的图象与x轴交于点A和B,与y轴交于点C.
22、如图,已知二次函数y=(1-m)x2+4x-3的图象与x轴交于点A和B,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 | 16 |
 在,请求出所有满足条件的D点坐标;若不存在,请说明理由.
在,请求出所有满足条件的D点坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,二次函数y=-x2+bx+c的图象经过坐标原点O和A(4,0).
如图所示,二次函数y=-x2+bx+c的图象经过坐标原点O和A(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知二次函数y=ax2-4x+c的图象与x轴交于点A(-1,0)、点C,与y轴交于点B(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与x轴交于点A(-1,0)、点C,与y轴交于点B(0,-5).查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 | 4 |
 你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么?
你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com