
【题目】![]() 、
、![]() 、
、![]() 、
、![]() 为矩形的四个顶点,
为矩形的四个顶点,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度向点
的速度向点![]() 移动,一直到达
移动,一直到达![]() 为止,点
为止,点![]() 以
以![]() 的速度向
的速度向![]() 移动.
移动.

(1)![]() 、
、![]() 两点从出发开始到几秒时四边形
两点从出发开始到几秒时四边形![]() 是矩形?
是矩形?
(2)![]() 、
、![]() 两点从出发开始到几秒时,点
两点从出发开始到几秒时,点![]() 和点
和点![]() 的距离是
的距离是![]() ?
?
【答案】(1)当![]() 、
、![]() 两点从出发开始到
两点从出发开始到![]() 秒时四边形
秒时四边形![]() 是矩形秒时四边形
是矩形秒时四边形![]() 为矩形;
为矩形;![]() ,
,![]() 两点从出发开始到
两点从出发开始到![]() 或
或![]() 秒时,点
秒时,点![]() ,
,![]() 间的距离是
间的距离是![]() .
.
【解析】
(1)当PB=CQ时,四边形PBCQ为矩形,依此建立方程求出即可;
(2)作PH⊥CD,垂足为H,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
(1)如图,∵A、B、C、D为矩形的四个顶点,
∴∠B=90°,AB∥CD,
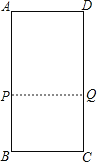
∴当PB=CQ时,四边形PBCQ为矩形,
设P、Q两点从出发开始到t秒时四边形PBCQ是矩形,
则16-3t=2t,
解得:t=![]() .
.
答:当![]() 、
、![]() 两点从出发开始到
两点从出发开始到![]() 秒时四边形
秒时四边形![]() 是矩形秒时四边形
是矩形秒时四边形![]() 为矩形;
为矩形;
![]() 设
设![]() ,
,![]() 两点从出发开始到
两点从出发开始到![]() 秒时,点
秒时,点![]() ,
,![]() 间的距离是
间的距离是![]() ,
,
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,
,
由勾股定理,得![]() ,
,
解得![]() ,
,![]() .
.
答:![]() ,
,![]() 两点从出发开始到
两点从出发开始到![]() 或
或![]() 秒时,点
秒时,点![]() ,
,![]() 间的距离是
间的距离是![]() .
.


科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲跑步中途改为步行,到达图书馆恰好用30 min.小东骑自行车以300 m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图9所示.
(1)家与图书馆之间的路程为 m,小玲步行的速度为 m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多好佳水果店在批发市场购买某种水果销售,第一次用1500元购进若干千克,并以每千克9元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1694元所购买的水果比第一次多20千克,以每千克10元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价45%售完剩余的水果.
(1)第一次水果的进价是每千克多少元?
(2)该水果店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距60km,甲从A地去B地,乙从B地去A地,图中![]() 、
、![]() 分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
分别表示甲、乙两人到B地的距离y(km)与甲出发时间x(h)的函数关系图象.
(1)根据图象,求乙的行驶速度.
(2)解释交点A的实际意义.
(3)求甲出发多少时间,两人之间恰好相距5km?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地间的直线公路长为![]() 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发
千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发![]() 小时,途中轿车出现了故障,停下维修,货车仍继续行驶.
小时,途中轿车出现了故障,停下维修,货车仍继续行驶.![]() 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离
小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离![]() (千米)与轿车所用的时间
(千米)与轿车所用的时间![]() (小时)的关系如图所示,请结合图象解答下列问题:
(小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是_______千米/小时;轿车的速度是_______千米/小时;![]() 值为_______.
值为_______.
(2)求轿车距其出发地的距离![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数关系式并写出自变量
(小时)之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)请直接写出货车出发多长时间两车相距![]() 千米.
千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面一段材料,再完成后面的问题:
材料:过抛物线y=ax2(a>0)的对称轴上一点(0,﹣![]() )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0,![]() )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,![]() ).
).
问题:若直线y=kx+b交抛物线y=![]() x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
①求抛物线y=![]() x2的焦点F的坐标;
x2的焦点F的坐标;
②求证:直线AB过焦点时,CF⊥DF;
③当直线AB过点(﹣1,0),且以线段AB为直径的圆与准线l相切时,求这条直线对应的函数解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com