(1)求证:不论m为何值,关于x的方程2x(x-2m)=(1-m)(1+m)总有两个不等的实数根.
(2)二次函数y=2x2-4mx+m2-1的图象与x轴有交点吗?请说明理由.
(3)请你根据前两问得到的启示,利用二次函数y=2x2-4x+1的图象,求出x取何值时y>0.
分析:(1)先把关于x的方程2x(x-2m)=(1-m)(1+m)化为一元二次方程的一般形式,再根据△>0时方程由两个不相等的实数根得到关于m的不等式,求出m的值即可;
(2)先求出△的表达式,再根据△的取值范围即可作出判断;
(3)先判断出抛物线的开口方向,再求出抛物线与x轴的两交点坐标,根据函数图象在x轴上方时y>0即可解答.
解答:解:(1)原方程可化为:2x
2-4mx+m
2-1=0,
∵△=(-4m)
2-4×2(m
2-1)=8m
2+8>0,
∴关于x的方程2x(x-2m)=(1-m)(1+m)总有两个不等的实数根;
(2)∵△=(-4m)
2-4×2(m
2-1)=8m
2+8>0,
∴二次函数y=2x
2-4mx+m
2-1的图象与x轴总有两个不同的交点;
(3)∵二次函数y=2x
2-4x+1中,a=2>0,
∴此函数的图象开口向上,
∵x=
=
=1±
,
∴二次函数y=2x
2-4x+1的图象与x轴的交点为(1+
,0),(1-
,0),
∴当x>1+
或x<
时y>0.
点评:本题考查的是二次函数的图象与x轴的交点问题,能把二次函数的解与解一元二次方程结合起来是解答此题的关键.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案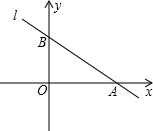 如图直线l:y=kx+2-4k(k为实数).
如图直线l:y=kx+2-4k(k为实数).