
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
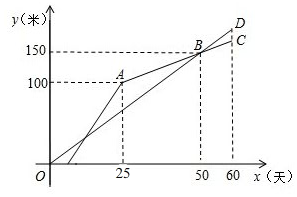 甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.
甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com