
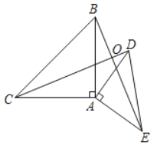
【题目】如图,△ABC与△ADE都是等腰直角三角形,连接CD、BE,CD、BE相交于点O,△BAE可看作是由△CAD顺时针旋转所得.
(1)旋转中心是 ,旋转角度是 ;
(2)判断CD与BE的位置关系,并说明理由.
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个红球和1个白球这些球除颜色外都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和红球是等可能的你同意吗?为什么.
(2)搅匀后从中一次摸出两个球,请通过列表或树状图求两个球是一红一白的概率;
(3)在这只袋中再放入若干个白球,搅匀后从中任意摸出一个球,要使摸出白球的概率为![]() ,应再放入多少个白球?
,应再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
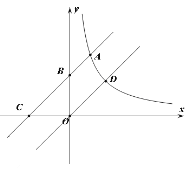
【题目】直线y=kx与反比例函数y=![]() (x>0)的图象相交点D(
(x>0)的图象相交点D(![]() ,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且
,m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A,与y轴交于点B,与x轴交于点C,且![]() ,求平移后的直线的表达式.
,求平移后的直线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
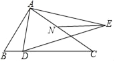
【题目】如图,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,点D是线段BC上一动点,连接AD,以AD为边作△ADE∽△ABC,点N是AC的中点,连接NE,当线段NE最短时,线段CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.

(1)求证:CD是⊙O的切线;
(2)若BC=8cm,tan∠CDA=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)条件下,过点B作⊙O的切线交CD的延长线于点E,连接OE,求四边形OEDA的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
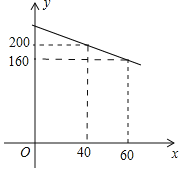
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足学生的个性化需求,新课程改革已经势在必行,某校积极开展拓展性课程建设,大体分为学科、文体、德育、其他等四个框架进行拓展课程设计。为了了解学生喜欢的拓展课程类型,学校随机抽取了部分学生进行调查,调查后将数据绘制成扇形统计图和条形统计图(未绘制完整).

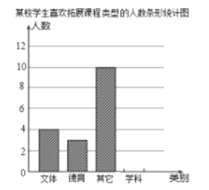
(1)求调查的学生总人数,并把条形图补充完整并填写扇形图中缺失的数据;
(2)小明同学说:“因为调查的同学中喜欢文体类拓展课程的同学占16%,而喜欢德育类拓展课程的同学仅占12%,所以全校2000名学生中,喜欢文体类拓展课程的同学人数一定比喜欢德育类拓展课程的同学人数多。”你觉得小明说得对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
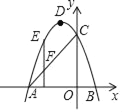
【题目】如图,在直角坐标系中,抛物线y=﹣(x+1)2+4与x轴交于点A、B,与y轴交于点C.
(1)写出抛物线顶点D的坐标 ;
(2)点D1是点D关于y轴的对称点,判断点D1是否在直线AC上,并说明理由;
(3)若点E是抛物线上的点,且在直线AC的上方,过点E作EF⊥x轴交线段AC于点F,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王叔叔家是养猪专业户,他们养的藏香猪和土黑猪一直很受市民欢迎.小王今年10月份开店卖猪肉,已知藏香猪肉售价每斤![]() 元,土黑猪肉售价每斤
元,土黑猪肉售价每斤![]() 元,每天固定从叔叔家进货两种猪肉共
元,每天固定从叔叔家进货两种猪肉共![]() 斤并且能全部售完.
斤并且能全部售完.
(1)若每天销售总额不低于![]() 元,则每天至少销售藏香猪肉多少斤?
元,则每天至少销售藏香猪肉多少斤?
(2)小王发现10月份每天上午就能将猪肉全部售完,而且消费者对猪肉的评价很高.于是小王决定调整猪肉价格,并增加进货量,且能将猪肉全部销售完.他将藏香猪肉的价格上涨![]() ,土黑猪肉的价格下调
,土黑猪肉的价格下调![]() ,销量与(1)中每天获得最低销售总额时的销量相比,藏香猪肉销量下降了
,销量与(1)中每天获得最低销售总额时的销量相比,藏香猪肉销量下降了![]() ,土黑猪肉销量是原来的
,土黑猪肉销量是原来的![]() 倍,结果每天的销售总额比(1)中每天获得的最低销售总额还多了
倍,结果每天的销售总额比(1)中每天获得的最低销售总额还多了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com