
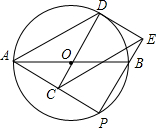
 如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF.
如图,AB是⊙O的直径,点P是AB下方的半圆上不与点A,B重合的一个动点,点C为AP中点,延长CO交⊙O于点D,连接AD,过点D作⊙O的切线交PB的廷长线于点E,连CE交AB于点F,连接DF.分析 (1)先由切线的性质得到∠CDE=90°,再利用垂径定理的推理得到DC⊥AP,接着根据圆周角定理得到∠APB=90°,于是可判断四边形DEPC为矩形,所以DC=EP,然后根据“SAS”判断△DAC≌△ECP;
(2)①根据全等三角形的性质得到AD=CE,∠DAC=∠ECP,根据平行线的判定得到AD∥CE,于是得到结论;②根据等腰三角形的性质得到∠DAO=∠ADO,根据平行线的性质得到∠ADO=∠DCF,等量代换得到∠DAO=∠DCF,推出A,C,F,D四点共圆,于是得到$\widehat{AC}$=$\widehat{DF}$,求得AC=DF,等量代换即可得到结论.
解答 (1)证明:∵DE为切线,
∴OD⊥DE,
∴∠CDE=90°,
∵点C为AP的中点,
∴DC⊥AP,
∴∠DCA=∠DCP=90°,
∵AB是⊙O直径,
∴∠APB=90°,
∴四边形DEPC为矩形,
∴DC=EP,
在△DAC和△ECP中
$\left\{\begin{array}{l}{AC=PC}\\{∠ACD=∠CPE}\\{DC=EP}\end{array}\right.$,
∴△DAC≌△ECP;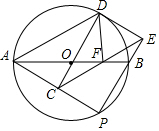
(2)①∵△DAC≌△ECP,
∴AD=CE,∠DAC=∠ECP,
∴AD∥CE,
∴四边形ACED是平行四边形;
②∵OA=OD,
∴∠DAO=∠ADO,
∵AD∥CE,
∴∠ADO=∠DCF,
∴∠DAO=∠DCF,
∴A,C,F,D四点共圆,
∴$\widehat{AC}$=$\widehat{DF}$,
∴AC=DF,
∵AC=$\frac{1}{2}$AP,
∴DF=$\frac{1}{2}$AP,
故答案为:DF=$\frac{1}{2}$AP.
点评 本题考查了切线的性质,平行四边形的判定和性质,全等三角形的判定和性质,四点共圆,熟练掌握切线的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
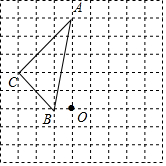 如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.
如图,在边长为1个单位长度的小正方形组成的9×9网格中,给出了格点△ABC(顶点是网格线交点),点O在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
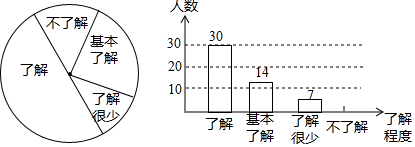
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
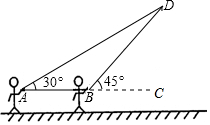 放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)
放风筝是大家喜爱的一项体育活动,星期天的上午小刚在市政府广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小刚迅速边收线边向前移动,到达了离A处10米的B处,此时风筝线的长度是多少米?(风筝线AD,BD均为线段,$\sqrt{2}$≈1.414.$\sqrt{3}$≈1.732,最后结果精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com