
【题目】中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
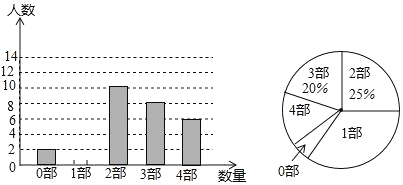
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是____部,中位数是_____部;
(2)扇形统计图中“4部”所在扇形的圆心角为_____度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
【答案】(1)1、2;(2)54;(3)补图见解析;(4)![]() .
.
【解析】
(1)先根据调查的总人数,求得1部对应的人数,进而得到本次调查所得数据的众数以及中位数;
(2)根据扇形圆心角的度数=部分占总体的百分比×360°,即可得到“4部”所在扇形的圆心角;
(3)根据1部对应的人数为40﹣2﹣10﹣8﹣6=14,即可将条形统计图补充完整;
(4)根据树状图所得的结果,判断他们选中同一名著的概率.
解:(1)∵调查的总人数为:10÷25%=40,
∴1部对应的人数为40﹣2﹣10﹣8﹣6=14,
∴本次调查所得数据的众数是1部,
∵2+14+10=26>21,2+14<20,
∴中位数为2部,
故答案为:1、2;
(2)扇形统计图中“4部”所在扇形的圆心角为:![]() ×360°=54°;
×360°=54°;
故答案为:54;
(3)条形统计图如图所示,
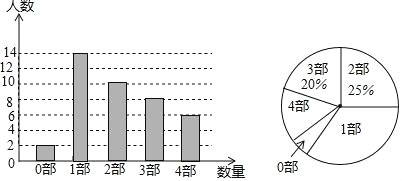
(4)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A,B,C,D,
画树状图可得:
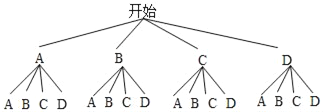
共有16种等可能的结果,其中选中同一名著的有4种,
故P(两人选中同一名著)=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 掷一枚均匀的骰子,骰子停止转动后,5点朝上是必然事件
B. 明天下雪的概率为![]() ,表示明天有半天都在下雪
,表示明天有半天都在下雪
C. 甲、乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
D. 了解一批充电宝的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
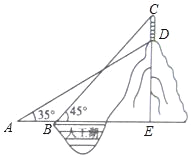
查看答案和解析>>
科目:初中数学 来源: 题型:
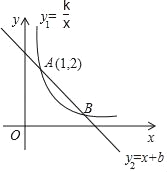
【题目】反比例函数y1=![]() (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.

(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,下面说法正确的个数是( )个.
①若O是△ABC的外心,∠A=50°,则∠BOC=100°;
②若O是△ABC的内心,∠A=50°,则∠BOC=115°;
③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;
④△ABC的面积是12,周长是16,则其内切圆的半径是1.

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是![]()
![]()
A. “打开电视机,正在播NBA篮球赛”是必然事件
B. “掷一枚硬币正面朝上的概率是![]() ”表示毎抛掷硬币2次就必有1次反面朝上
”表示毎抛掷硬币2次就必有1次反面朝上
C. 一组数据2,3,4,5,5,6的众数和中位数都是5
D. 甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中:
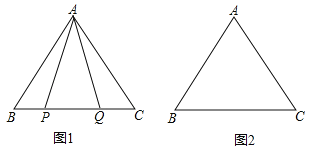
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知二次函数![]() 的图象过点
的图象过点![]() .
.
![]() 若
若![]() ,求函数的表达式;
,求函数的表达式;
![]() 若函数图象的顶点在x轴上,求a的值;
若函数图象的顶点在x轴上,求a的值;
![]() 已知点
已知点![]() 和
和![]() 都在该函数图象上,试比较m、n的大小.
都在该函数图象上,试比较m、n的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com