
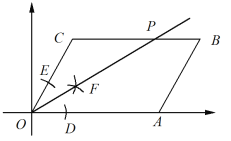
【题目】如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,OC=4,∠AOC=60°,且以点O为圆心,任意长为半径画弧,分别交OA、OC于点D、E;再分别以点D、点E为圆心,大于![]() DE的长度为半径画弧,两弧相交于点F,过点O作射线OF,交BC于点P.则点P的坐标为( )
DE的长度为半径画弧,两弧相交于点F,过点O作射线OF,交BC于点P.则点P的坐标为( )
A.(4,2![]() )B.(6,2
)B.(6,2![]() )C.(2
)C.(2![]() ,4)D.(2
,4)D.(2![]() ,6)
,6)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在某海域,一般指挥船在C处收到渔船在B处发出的求救信号,经确定,遇险抛锚的渔船所在的B处位于C处的南偏西45°方向上,且BC=60海里;指挥船搜索发现,在C处的南偏西60°方向上有一艘海监船A,恰好位于B处的正西方向.于是命令海监船A前往搜救,已知海监船A的航行速度为30海里/小时,问渔船在B处需要等待多长时间才能得到海监船A的救援?(参考数据:![]() ,
,![]() ,
,![]() 结果精确到0.1小时)
结果精确到0.1小时)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的一条弦,
的一条弦,![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,且恰好
,且恰好![]() ∥
∥![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
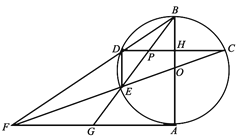
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)求证:点![]() 是
是![]() 的中点;
的中点;
(3)当⊙![]() 的半径为
的半径为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
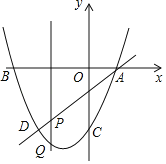
【题目】如图,抛物线y=ax2+bx﹣3过A(1,0),B(﹣3,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点.
(1)求直线AD及抛物线的解析式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P,Q,D,R为顶点的四边形是平行四边形?若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
(收集数据)
(1)若要从全年级学生中抽取一个48人的样本,你认为以下抽样方法中比较合理的有 ;(只要填写序号即可)
①随机抽取一个班级的48名学生;②在全年级学生中随机抽取48名学生;③在全年级12个班中分别各抽取4名学生;④从全年级学生中随机抽取48名男生;
(整理数据)
(2)将抽取的48名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 、
②估计全年级A、B类学生大约一共有 名;

成绩(分) | 频数 | 频率 |
A类(80~100) | 0.5 | |
B类(60~79) | 0.25 | |
C类(40~59) | 8 | |
D类(0~39) | 4 |
(3)学校为了解其他学校教学情况,将同层次的第一、第二两所中学的抽样数据进行对比,得下表:
学校 | 平均分(分) | 极差(分) | 方差 | A、B类的频率和 |
第一中学 | 71 | 52 | 432 | 0.75 |
第二中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校的教学效果较好?结合数据,请给出一个解释来支持你的观点.
查看答案和解析>>
科目:初中数学 来源: 题型:
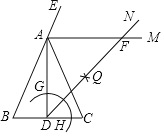
【题目】如图,在△ABC中,AB=AC,AD是高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于![]() GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则△ADF的形状是( )
GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则△ADF的形状是( )
A.等腰三角形B.等边三角形
C.直角三角形D.等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
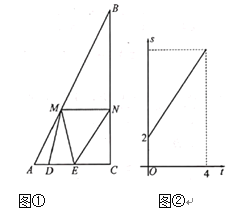
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() 点
点![]() 是
是![]() 上位于点
上位于点![]() 右侧的动点,点
右侧的动点,点![]() 是
是![]() 上的动点,在运动过程中始终保持
上的动点,在运动过程中始终保持![]() ,
,![]() cm.过
cm.过![]() 作
作![]() 交
交![]() 于
于![]() ,当点
,当点![]() 与点
与点![]() 重合时点
重合时点![]() 停止运动.设
停止运动.设![]() 的而积为
的而积为![]() ,点
,点![]() 的运动时问为
的运动时问为![]() ,
,![]() 与
与![]() 的函数关系如图②所示:
的函数关系如图②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
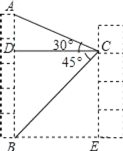
【题目】小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com