
【题目】2016年12月28日举行了微山县南阳镇北、两城镇南跨湖高速的路线开工仪式,其中的一项工程由A、B两工程队合作,120天可以完成;如果A,B两工程队单独完成此项工程,B工程队所用时间是A工程队的1.5倍.
(1)求A,B两工程队单独完成此项工程各需多少天?
(2)在施工过程中,该总公司派一名技术人员在现场对施工质量进行全程监督,每天总公司补助技术人员100元,若由A工程队单独施工,平均每天A工程队的费用为0.5万元,现总公司选择了B工程队单独施工,要求总费用不能超过选择A工程队时的总费用,则平均每天B工程队的费用最多为多少?
【答案】
(1)解:设A单独完成需要x天,则B单独完成需要1.5x天,由题意得:
![]() +
+ ![]() =
= ![]() ,
,
解得:x=200,
经检验,x=200是原方程的解.
则B单独完成需要天数:20×1.5=30(天).
答:A单独完成需要20天,则B单独完成需要30天
(2)解:A工程队需要费用为:0.5×200+0.01×200=102(万元);
设B工程队每天的施工费用为y万元,则:300y+300×0.01≤102,
解得:y≤0.33,
所以B工程队每天的施工费用为0.33万元
【解析】(1)首先设A单独完成需要x天,则B单独完成需要1.5x天,根据A、B两工程队合作,120天可以完成,列出分式方程,求解即可;(2)先求出A工程队需要的总费用,再设B工程队每天的施工费用为y万元,根据B工程队单独施工,要求总费用不能超过选择A工程队时的总费用,列出不等式,求解即可得出答案.
【考点精析】解答此题的关键在于理解分式方程的应用的相关知识,掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图1所示,点E为矩形ABCD边AD的中点,在矩形ABCD的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员P从点B出发,沿着B﹣E﹣D的路线匀速行进,到达点D.设运动员P的运动时间为t,到监测点的距离为y.现有y与t的函数关系的图象大致如图2所示,则这一信息的来源监测点为( )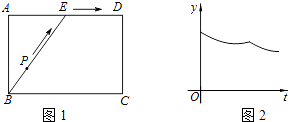
A.A点
B.B点
C.C点
D.D点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a>b,请用“>”或“<”填空:
(1)a-1________b-1;(2)![]() a________
a________![]() b;(3)a+c________b+c;(4)-3a________-3b;(5)-
b;(3)a+c________b+c;(4)-3a________-3b;(5)-![]() a-c________-
a-c________-![]() b-c.
b-c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F. 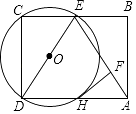
(1)求证:HF是⊙O的切线;
(2)若DH=3,AF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
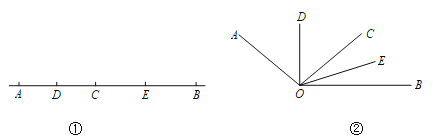
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com