
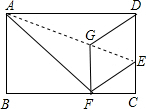
 如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.
如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.分析 (1)根据折叠的性质,易知DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,易证FG=FE,故由四边相等证明四边形DEFG为菱形;
(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出$\frac{CE}{DE}$的值.
解答 (1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,
∵FG∥CD,
∴∠2=∠3,
∴FG=FE,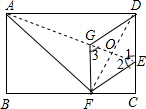
∴DG=GF=EF=DE,
∴四边形DEFG为菱形;
(2)解:设DE=x,根据折叠的性质,EF=DE=x,EC=8-x,
在Rt△EFC中,FC2+EC2=EF2,
即42+(8-x)2=x2,
解得:x=5,CE=8-x=3,
∴$\frac{CE}{DE}$=$\frac{3}{5}$.
点评 本题主要考查了折叠的性质、菱形的判定以及勾股定理,熟知折叠的性质和菱形的判定方法是解答此题的关键.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | x6÷x2=x3 | B. | (-x)-1=$\frac{1}{x}$ | C. | (2x3)2=4x6 | D. | -2a2•a3=-2a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
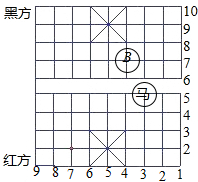 观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:(4,7).
观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进四”后到达B点,则表示B点位置的数对是:(4,7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
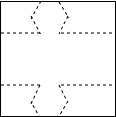 如图,将一张边长为6cm的正方形纸片按虚线裁剪后,恰好围成底面是正六边形的棱柱,则这个六棱柱的侧面积为36-12$\sqrt{3}$cm2.
如图,将一张边长为6cm的正方形纸片按虚线裁剪后,恰好围成底面是正六边形的棱柱,则这个六棱柱的侧面积为36-12$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
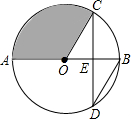 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积为( )| A. | π | B. | 4π | C. | $\frac{4}{3}$π | D. | $\frac{16}{3}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
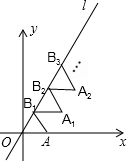 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是($\frac{2017}{2}$,$\frac{2015\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是($\frac{2017}{2}$,$\frac{2015\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
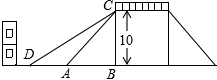 如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=$\sqrt{3}$:3.若新坡角外需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com