
【题目】(1)知识延伸:如图1,在![]() 中,
中,![]() ,
,![]() ,根据三角函数的定义得:
,根据三角函数的定义得:![]() ;
;
(2)拓展运用:如图2,在锐角三角形![]() 中,
中,![]() .
.
①求证:![]() ;
;
②已知:![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)1;(2) ①见解析;②60°.
【解析】分析:(1)利用三角函数定义直接计算即可;
(2)①过A作AD⊥BC于点D,设BD=x,则CD=a﹣x,利用勾股定理可分别表示出AD,整理则可证得结论;
②直接代入①中所得结论,可求得cosB的值,则可求得∠B的度数.
详解:(1)∵在△ABC中,∠C=90°,AB=c,BC=a,AC=b,∴sinA=![]() ,cosA=
,cosA=![]() ,且a2+b2=c2,∴sin2A+cos2A=(
,且a2+b2=c2,∴sin2A+cos2A=(![]() )2+(
)2+(![]() )2=
)2=![]() =
=![]() =1.
=1.
故答案为:1;
(2)①过A作AD⊥BC于点D,如图,设BD=x,则CD=a﹣x.在Rt△ABD中,由勾股定理可得AD2=AB2﹣BD2.在Rt△ACD中,由勾股定理可得AD2=AC2﹣CD2,∴AB2﹣BD2=AC2﹣CD2,即c2﹣x2=b2﹣(a﹣x)2,∴b2=a2+c2﹣2ax.在Rt△ABD中,cosB=![]() ,∴x=ccosB,∴b2=a2+c2﹣2accosB;
,∴x=ccosB,∴b2=a2+c2﹣2accosB;
②当a=3,b=![]() ,c=2时,代入①中结论,可得(
,c=2时,代入①中结论,可得(![]() )2=32+22﹣2×3×2cosB,∴cosB=
)2=32+22﹣2×3×2cosB,∴cosB=![]() ,∴∠B=60°.
,∴∠B=60°.


科目:初中数学 来源: 题型:
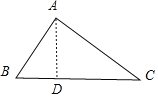
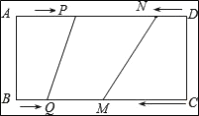
【题目】如图,在矩形ABCD中,BC=24cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.
已知在相同时间内,若BQ=x cm(x≠0),则AP=2x cm,CM=3x cm,DN=x2cm.
(1)当x为何值时,以P、N两点重合?
(2)问Q、M两点能重合吗?若Q、M两点能重合,则求出相应的x的值;若Q、M两点不能重合,请说明理由.
(3)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个数用大括号围起来,中间用逗号隔开.如:![]() ,我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数-4-a也必是这个集合的元素,这样的集合我们称为友好集合.
,我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数-4-a也必是这个集合的元素,这样的集合我们称为友好集合.
(1)请你判断集合![]() ,
,![]() 是不是友好集合?
是不是友好集合?
(2)请你写出满足条件的两个友好集合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(0,1),B(0,![]() ),C(3,0).
),C(3,0).

(1)若以A、B、C、D为顶点的四边形是平行四边形,则请你写出所有符合条件的D点坐标.
(2)直接写出一个符合(1)中条件的直线AD 的解析式.
(3)求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 以
以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒
秒![]() .
.
![]()
(1)当![]() 时,求线段
时,求线段![]() 和
和![]() 的长度.
的长度.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 中点为
中点为![]() ,则
,则![]() 的长是否变化?若不变.求出
的长是否变化?若不变.求出![]() 的长;若发生变化,请说明理由.
的长;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
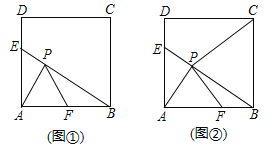
【题目】如图,边长为6的正方形![]() 中,
中,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,
,![]() 为垂足.
为垂足.
(1)如图①, AF=BF,AE=2![]() ,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
,点T是射线PF上的一个动点,则当△ABT为直角三角形时,求AT的长;
(2)如图②,若![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
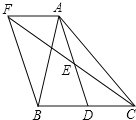
【题目】如图,在![]() 中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且
中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且![]() ,连接BF.
,连接BF.
![]() 证明:
证明:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形AFBD是矩形?并说明理由.
满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com