【题目】如图，将一等边三角形的三条边各8等分，按顺时针方向（图中箭头方向）标注各等分点的序号0、1、2、3、4、5、6、7、8，将不同边上的序号和为8的两点依次连接起来，这样就建立了“三角形”坐标系．在建立的“三角形”坐标系内，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始，按顺时针方向），如点
的坐标可表示为（1，2，5），点
的坐标可表示为（4，1，3），按此方法，则点
的坐标可表示为（ ）
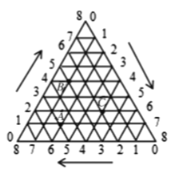
A.
B.
C.
D.
科目：初中数学 来源： 题型：
【题目】如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，则S△CDF：S四边形ABFE等于（ ）
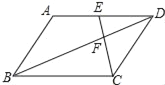
A. 1：3 B. 2：5 C. 3：5 D. 4：9
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A，B，C都在抛物线y=ax2﹣2amx+am2+2m﹣5（其中﹣
＜a＜0）上，AB∥x轴，∠ABC=135°，且AB=4．
（1）填空：抛物线的顶点坐标为 （用含m的代数式表示）；
（2）求△ABC的面积（用含a的代数式表示）；
（3）若△ABC的面积为2，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在同一条道路上，甲车从
地到
地，乙车从地到地，乙先出发，图中的折线段表示甲、乙两车之间的距离
（千米）与行驶时间
（小时）的函数关系的图象，根据图象解决以下问题：
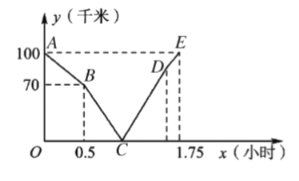
（1）乙先出发的时间为 小时，乙车的速度为 千米/时；
（2）求线段
的函数关系式，并写出自变量的取值范围；
（3）甲、乙两车谁先到终点，先到多少时间？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一张矩形纸片ABCD，其中AD＝8cm，AB＝6cm，先沿对角线BD对折，点C落在点C′的位置，BC′交AD于点G．
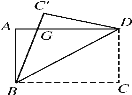
(1)求证：AG＝C′G；
(2) 求△BDG的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】知识背景
我们在第十一章《三角形》中学习了三角形的边与角的性质，在第十二章《全等三角形》中学习了全等三角形的性质和判定，在十三章《轴对称》中学习了等腰三角形的性质和判定．在一些探究题中经常用以上知识转化角和边，进而解决问题
问题初探
如图（1），△ABC中，∠BAC＝90°，AB＝AC，点D是BC上一点，连接AD，以AD为一边作△ADE，使∠DAE＝90°，AD＝AE，连接BE，猜想BE和CD有怎样的数量关系，并说明理由．
类比再探
如图（2），△ABC中，∠BAC＝90°，AB＝AC，点M是AB上一点，点D是BC上一点，连接MD，以MD为一边作△MDE，使∠DME＝90°，MD＝ME，连接BE，则∠EBD＝ ．（直接写出答案，不写过程，但要求作出辅助线）
方法迁移
如图（3），△ABC是等边三角形，点D是BC上一点，连接AD，以AD为一边作等边三角形ADE，连接BE，则BD、BE、BC之间有怎样的数量关系？ （直接写出答案，不写过程）．
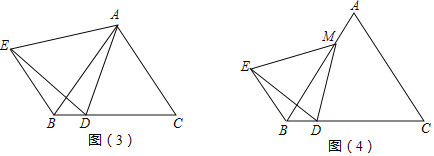
拓展创新
如图（4），△ABC是等边三角形，点M是AB上一点，点D是BC上一点，连接MD，以MD为一边作等边三角形MDE，连接BE．猜想∠EBD的度数，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠1=∠2，则下列条件中不一定能使△ABC≌△ABD的是( )
A. AC=AD B. BC=BD C. ∠C=∠D D. ∠3=∠4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
