
【题目】在平面直角坐标系中,抛物线y=﹣x2+2bx+c与x轴交于点A、B(点A在点B的右侧),且与y轴正半轴交于点C,已知A(2,0) 
(1)当B(﹣4,0)时,求抛物线的解析式;
(2)O为坐标原点,抛物线的顶点为P,当tan∠OAP=3时,求此抛物线的解析式;
(3)O为坐标原点,以A为圆心OA长为半径画⊙A,以C为圆心, ![]() OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
OC长为半径画圆⊙C,当⊙A与⊙C外切时,求此抛物线的解析式.
【答案】
(1)解:把点A(2,0)、B(﹣4,0)的坐标代入y=﹣x2+2bx+c得, ![]() ,
,
∴b=﹣1.c=8,
∴抛物线的解析式为y=﹣x2﹣2x+8
(2)解:如图1,
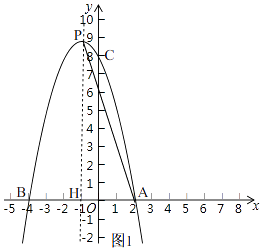
设抛物线的对称轴与x轴的交点为H,把点A(2,0)的坐标代入y=﹣x2+2bx+c得,
﹣4+4b+c=0①,
∵抛物线的顶点为P,
∴y=﹣x2+2bx+c=﹣(x﹣b)2+b2+c,
∴P(b,b2+c),
∴PH=b2+c,AH=2﹣b,
在Rt△PHA中,tan∠OAP= ![]() ,
,
∴ ![]() =3②,
=3②,
联立①②得, 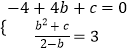 ,
,
∴ ![]() (不符合题意,舍)或
(不符合题意,舍)或 ![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+8
(3)解:∵如图2,
抛物线y=﹣x2+2bx+c与y轴正半轴交于点C,
∴C(0,c)(c>0),
∴ ![]() OC=
OC= ![]() c,
c,
∵A(2,0),
∴OA=2,
∴AC= ![]() ,
,
∵⊙A与⊙C外切,
∴AC= ![]() c+2=
c+2= ![]() ,
,
∴c=0(舍)或c= ![]() ,
,
把点A(2,0)的坐标代入y=﹣x2+2bx+c得,﹣4+4b+c=0,
∴b= ![]() ,
,
∴抛物线的解析式为y=﹣x2+ ![]() x+
x+ ![]() .
.
【解析】(1)利用待定系数法即可确定出函数解析式;(2)用tan∠OAP=3建立一个b,c的关系,再结合点A得出的等式即可求出b,c进而得出函数关系式;(3)用两圆外切,半径之和等于AC建立方程结合点A代入建立的方程即可得出抛物线解析式.


科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在Rt△ABC和Rt△A'B'C'中,AB=A'B',AC=A'C',C=∠C'=90°.
求证:Rt△ABC和Rt△A'B'C'全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A'B'C'拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A'重合,点C与点C'重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
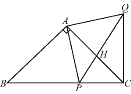
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点P是BC上的一动点,AP=AQ,∠PAQ=90°,连接CQ.
(1)求证:CQ⊥BC.
(2)△ACQ能否是直角三角形?若能,请直接写出此时点P的位置;若不能,请说明理由.
(3)当点P在BC上什么位置时,△ACQ是等腰三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF. 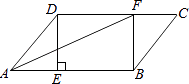
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com