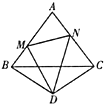
【题目】如图，有边长为1的等边三角形
和顶角为120°的等腰
，以
为顶点作
角，两边分别交
、
于
、
，连结
，则
的周长为________.
【答案】2
【解析】
要求△AMN的周长，根据题目已知条件无法求出三条边的长，只能把三条边长用其它已知边长来表示，所以需要作辅助线，延长AB至F，使BF=CN，连接DF，通过证明△BDF≌△CND，及△DMN≌△DMF，从而得出MN=MF，△AMN的周长等于AB+AC的长．
∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°，
∵△ABC是边长为1的等边三角形，
∴∠ABC=∠BAC=∠BCA=60°，
∴∠DBA=∠DCA=90°，
延长AB至F，使BF=CN，连接DF，
在△BDF和△CND中，
∵
，
∴△BDF≌△CND(SAS)，
∴∠BDF=∠CDN，DF=DN，
∵∠MDN=60°，
∴∠BDM+∠CDN=60°，
∴∠BDM+∠BDF=60°，
在△DMN和△DMF中，
∵
，
∴△DMN≌△DMF(SAS)
∴MN=MF，
∴△AMN的周长是：
AM+AN+MN=AM+MB+BF+AN=AB+AC=1+1=2，
故答案为：2
中考解读考点精练系列答案
各地期末复习特训卷系列答案科目：初中数学 来源： 题型：
【题目】探究活动：
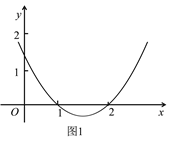
利用函数
的图象(如图1)和性质，探究函数
的图象与性质．
下面是小东的探究过程，请补充完整：
（1）函数的自变量x的取值范围是___________；
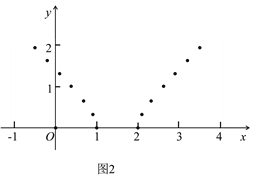
（2）如图2，小东列表描出了函数图象上部分点，请画出函数图象；
（3）解决问题：设方程
的两根为
、
，且
，方程
的两根为
、
，且
．若
，则、、、的大小关系为_____________________（用“<”连接）．
查看答案和解析>>
科目：初中数学 来源： 题型：
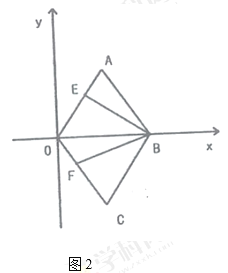
【题目】四边形
是菱形，
，
（1）如图1，作
的平分线
，交
于
（不写作法和证明，保留作图痕迹）
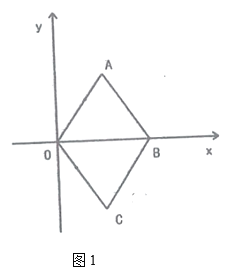
（2）在（1）的条件下，点
在直线上，
最大值时，求
的长
（3）如图2，
，
分别是线段
，
上的动点，
，求四边形
周长的最小值.
查看答案和解析>>
科目：初中数学 来源： 题型：
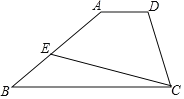
【题目】在四边形ABCD中，AD∥BC，E为AB边上一点，∠BCE=16°，EF∥BC交DC于点F．
（1）依题意补全图形，并求∠FEC的度数；
（2）若∠A=141°，求∠AEC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于平面直角坐标系xOy中的任意两点M(x1，y1)，N(x2，y2)，给出如下定义：
将|x1﹣x2|称为点M，N之间的“横长”，|y1﹣y2|称为点M，N之间的纵长”，点M与点N的“横长”与“纵长”之和称为“折线距离”，记作d(M，N)=|x1﹣x2|+|y1﹣y2|“．
例如：若点M(﹣1，1)，点N(2，﹣2)，则点M与点N的“折线距离”为：d(M，N)=|﹣1﹣2|+|1﹣(﹣2)|=3+3=6．
根据以上定义，解决下列问题：
已知点P(3，2)．
（1）若点A(a，2)，且d(P，A)=5，求a的值；
（2）已知点B(b，b)，且d(P，B)＜3，直接写出b的取值范围；
（3）若第一象限内的点T与点P的“横长”与“纵长”相等，且d(P，T)＞5，简要分析点T的横坐标t的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们在学习《从面积到乘法公式》时，曾用两种不同的方法计算同一个图形的面积，探索了单项式乘多项式的运算法则：m（a+b+c）＝ma+mb+mc（如图1），多项式乘多项式的运算法则：
（a+b）（c+d）＝ac+ad+bc+bd（如图2），以及完全平方公式：（a+b）2＝a2+2ab+b2（如图3）．
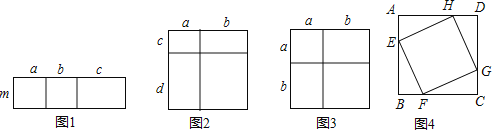
把几个图形拼成一个新的图形，通过图形面积的计算，常常可以得到一些等式，这是研究数学问题的一种常用方法．
（1）请设计两个图形说明一下两个等式成立（画出示意图，并标上字母）
①（a+b）（2a+b）＝2a2+3ab+b2
②（a+b+c）2＝a2+b2+c2+2ab+2ac+2bc
（2）如图4，它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD．如果每个直角三角形的较短的边长为a，较长的边长为b，最长的边长为c．试用两种不同的方法计算这个大正方形的面积，你能发现直角三角形的三边长a、b、c的什么数量关系？（注：写出解答过程）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
