
°æƒø°ø“—÷™≈◊ŒÔœþy£Ωx2©Åmx+næ≠π˝µ„A£®3£¨0£©£Æ
£®1£©µ±m+n£Ω©Å1 ±£¨«Û∏√≈◊ŒÔœþµƒΩ‚Œˆ Ω∫Õ∂•µ„◊¯±Í£ª
£®2£©µ±Bµ„◊¯±ÍŒ™£®0£¨©Å3£© ±£¨»Ù≈◊ŒÔœþy£Ωx2©Åmx+nÕºœÛµƒ∂•µ„‘⁄÷±œþAB…œ£¨«Ûm°¢nµƒ÷µ£ª
£®3£©¢Ÿ…Ëm£Ω©Å2£¨µ±0°Ðx°Ð3 ±£¨«Û≈◊ŒÔœþy£Ωx2©Åmx+nµƒ◊Ó–°÷µ£ª
¢⁄»Ùµ±0°Ðx°Ð3 ±£¨∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒ◊Ó–°÷µŒ™©Å4£¨«Ûm°¢nµƒ÷µ£Æ
°æ¥∞∏°ø£®1£©y£Ωx2©Å2x©Å3£¨∂•µ„◊¯±ÍŒ™£®1£¨©Å4£©£ª£®2£©![]() ªÚ
ªÚ![]() £ª£®3£©¢Ÿ-15£ª¢⁄m£Ω2£¨n£Ω©Å3£Æ
£ª£®3£©¢Ÿ-15£ª¢⁄m£Ω2£¨n£Ω©Å3£Æ
°æΩ‚Œˆ°ø
£®1£©Ω´µ„A£®3£¨0£©¥˙»ÎΩ‚Œˆ Ω£¨µ√9©Å3m+n£Ω0£¨”Îm+n£Ω1◊È≥…∑Ω≥Ã◊È£¨Ω‚∑Ω≥Ã◊È«Ûµ√m°¢nº¥ø…£ª
£®2£©œ»±Ì æ≥ˆ∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nÕºœÛµƒ∂•µ„£¨¿˚”√÷±œþAB¡–≥ˆ Ω◊”£¨‘Ÿ”ε„A‘⁄∂˛¥Œ∫Ø ˝…œµ√µΩµƒ Ω◊”◊È≥…∑Ω≥Ã◊È«Ûµ√m£¨nµƒ÷µ£¨
£®3£©¢Ÿ“◊«Û≈◊ŒÔœþΩ‚Œˆ ΩŒ™y£Ωx2+2x©Å15£Æ∏˘æð≈◊ŒÔœþµƒ∂‘≥∆–‘∫Õ‘ˆºı–‘¿¥«Û∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒ◊Ó–°÷µ£ª
¢⁄±æ“™∑÷»˝÷÷«Èøˆ£∫µ±∂‘≥∆÷·![]() ±£ªµ±∂‘≥∆÷·
±£ªµ±∂‘≥∆÷·![]() ±£ªµ±∂‘≥∆÷·
±£ªµ±∂‘≥∆÷·![]() ±£¨Ω·∫œ∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒÕºœÛæ≠π˝µ„Aµ√≥ˆ Ω◊”9©Å3m+n£Ω0£¨«Û≥ˆm£¨nµ´“ª∂®“™—È÷§ «∑Ò∑˚∫œÃ‚“‚£Æ
±£¨Ω·∫œ∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒÕºœÛæ≠π˝µ„Aµ√≥ˆ Ω◊”9©Å3m+n£Ω0£¨«Û≥ˆm£¨nµ´“ª∂®“™—È÷§ «∑Ò∑˚∫œÃ‚“‚£Æ
Ω‚£∫£®1£©Ω´µ„A£®3£¨0£©¥˙»Îy£Ωx2©Åmx+n÷–£¨µ√9©Å3m+n£Ω0£¨
”÷°þm+n£Ω©Å1£¨
°ý![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y£Ωx2©Å2x©Å3£¨
°þy£Ωx2©Å2x©Å3£Ω£®x©Å1£©2©Å4£¨
°ý∂•µ„◊¯±ÍŒ™£®1£¨©Å4£©£Æ
£®2£©∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nÕºœÛµƒ∂•µ„◊¯±ÍŒ™![]() £¨
£¨
…Ë÷±œþABµƒΩ‚Œˆ ΩŒ™y£Ωkx+b£¨Ω´A£®3£¨0£©£¨B£®0£¨©Å3£©¥˙»Îµ√![]() £¨
£¨
Ω‚µ√![]()
°ý÷±œþABµƒΩ‚Œˆ ΩŒ™y£Ωx©Å3£¨
°þ≈◊ŒÔœþ∂•µ„![]() ‘⁄÷±œþAB…œ£¨
‘⁄÷±œþAB…œ£¨
°ýµ√![]() £¨
£¨
”÷°þ∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒÕºœÛæ≠π˝µ„A£®3£¨0£©£¨
°ý9©Å3m+n£Ω0£¨
°ý¡™¡¢∑Ω≥Ã◊ȵ√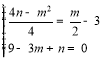 £¨Ω‚µ√
£¨Ω‚µ√![]() ªÚ
ªÚ![]() £ª
£ª
£®3£©¢Ÿ°þ∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒÕºœÛæ≠π˝µ„A£®3£¨0£©£¨
°ý9©Å3m+n£Ω0£¨
µ±m£Ω©Å2 ±£¨Ω‚µ√n£Ω©Å15£¨
°ý∂˛¥Œ∫Ø ˝µƒΩ‚Œˆ ΩŒ™y£Ωx2+2x©Å15£¨
°þ∂‘≥∆÷·x£Ω©Å1‘⁄0°Ðx°Ð3µƒ◊Û≤ý£¨«“∂˛¥Œ∫Ø ˝µƒÕºœÛø™ø⁄œÚ…œ£¨
°ýx£Ω0 ±£¨y»°◊Ó–°÷µ£¨◊Ó–°÷µ «©Å15£Æ
°ýµ±0°Ðx°Ð3 ±£¨∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒ◊Ó–°÷µŒ™©Å15£ª
¢⁄∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nÕºœÛµƒ∂‘≥∆÷·Œ™÷±œþx£Ω![]() £¨∂•µ„◊¯±ÍŒ™
£¨∂•µ„◊¯±ÍŒ™![]() £¨
£¨
¢°£©µ±∂‘≥∆÷·![]() °ð3 ±£¨º¥m°ð6 ±£¨‘⁄0°Ðx°Ð3÷–£¨∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒ◊Ó–°÷µµƒ◊Ó–°÷µŒ™0£¨¥À÷÷«Èøˆ≤ª∫œÃ‚“‚£ª
°ð3 ±£¨º¥m°ð6 ±£¨‘⁄0°Ðx°Ð3÷–£¨∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒ◊Ó–°÷µµƒ◊Ó–°÷µŒ™0£¨¥À÷÷«Èøˆ≤ª∫œÃ‚“‚£ª
¢¢£©µ±∂‘≥∆÷·0£º![]() £º3 ±£¨º¥0£ºm£º6 ±£¨
£º3 ±£¨º¥0£ºm£º6 ±£¨
 Ω‚µ√
Ω‚µ√![]() ªÚ
ªÚ![]() £®…·»•£©
£®…·»•£©
°ým£Ω2£¨n£Ω©Å3£ª
¢££©µ±∂‘≥∆÷·![]() °Ð0 ±£¨º¥m°Ð0 ±£¨
°Ð0 ±£¨º¥m°Ð0 ±£¨
![]() Ω‚µ√
Ω‚µ√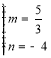 £®…·»•£©£¨
£®…·»•£©£¨
◊€…œÀ˘ ˆµ±0°Ðx°Ð3 ±£¨∂˛¥Œ∫Ø ˝y£Ωx2©Åmx+nµƒ◊Ó–°÷µŒ™©Å4 ±£¨m£Ω2£¨n£Ω©Å3£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øæ≠π˝ƒ≥ Æ◊÷¬∑ø⁄µƒ∆˚≥µ£¨ø…ƒÐ÷±––£¨“≤ø…ƒÐœÚ◊Û◊™ªÚœÚ”“◊™£Æ»Áπ˚’‚»˝÷÷ø…ƒÐ–‘¥Û–°œýÕ¨£¨œ÷”–¡Ω¡æ∆˚≥µæ≠π˝’‚∏ˆ Æ◊÷¬∑ø⁄£Æ
£®1£©”√ª≠ ˜◊¥Õº∑®ªÚ¡–±Ì∑®∑÷Œˆ’‚¡Ω¡æ∆˚≥µ–– ª∑ΩœÚÀ˘”–ø…ƒÐµƒΩ·π˚£ª
£®2£©«Û“ª¡æ≥µœÚ”“◊™£¨“ª¡æ≥µœÚ◊Û◊™µƒ∏≈¬ £ª
£®3£©«Û÷¡…Ÿ”–“ª¡æ≥µ÷±––µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄![]() ÷–£¨
÷–£¨![]() £¨µ„
£¨µ„![]() °¢
°¢![]() °¢
°¢![]() ∑÷±‘⁄
∑÷±‘⁄![]() °¢
°¢![]() °¢
°¢![]() ±þ…œ£¨“‘
±þ…œ£¨“‘![]() Œ™÷±æ∂°—
Œ™÷±æ∂°—![]() µƒ«°∫√æ≠π˝
µƒ«°∫√æ≠π˝![]() °¢
°¢![]() £¨«“
£¨«“![]()
£®1£©«Û÷§£∫![]() Œ™°—
Œ™°—![]() µƒ«–œþ£ª
µƒ«–œþ£ª
£®2£©»Ù![]() £¨«Û
£¨«Û![]() µƒ∂» ˝£ª
µƒ∂» ˝£ª
£®3£©»Ù![]() £¨
£¨![]() £¨«Û°—
£¨«Û°—![]() µƒ∞Îæ∂º∞œþ∂Œ
µƒ∞Îæ∂º∞œþ∂Œ![]() µƒ≥§
µƒ≥§

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘ƒ∂¡∂‘—ß…˙µƒ≥…≥§”–◊≈…Ó‘∂µƒ”∞œÏ£¨ƒ≥÷–—ߌ™¡ÀΩ‚—ß…˙√ø÷ÐøŒ”ý‘ƒ∂¡µƒ ±º‰£¨‘⁄±æ–£Àʪ˙≥È»°¡À»Ù∏…√˚—ß…˙Ω¯––µ˜≤È£¨≤¢“¿æðµ˜≤ÈΩ·π˚ªÊ÷∆¡À“‘œ¬≤ªÕÍ’˚µƒÕ≥º∆Õº±Ì£Æ
◊ȱ | ±º‰£®–° ±£© | ∆µ ˝£®»À ˝£© | ∆µ¬ |
A | 0°Ðt°Ð0.5 | 6 | 0.15 |
B | 0.5°Ðt°Ð1 | a | 0.3 |
C | 1°Ðt°Ð1.5 | 10 | 0.25 |
D | 1.5°Ðt°Ð2 | 8 | b |
E | 2°Ðt°Ð2.5 | 4 | 0.1 |
∫œº∆ | 1 |
«Î∏˘æðÕº±Ì÷–µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©±Ì÷–µƒa= £¨b= £¨÷–Œª ˝¬‰‘⁄ ◊È£¨Ω´∆µ ˝∑÷≤º÷±∑ΩÕº≤π»´£ª
£®2£©π¿º∆∏√–£2000√˚—ß…˙÷–£¨√ø÷ÐøŒ”ý‘ƒ∂¡ ±º‰≤ª◊„0.5–° ±µƒ—ß…˙¥Û‘º”–∂ý…Ÿ√˚£ø
£®3£©E◊ȵƒ4»À÷–£¨”–1√˚ƒ–…˙∫Õ3√˚≈Æ…˙£¨∏√–£º∆ªÆ‘⁄E◊È—ß…˙÷–Àʪ˙—°≥ˆ¡Ω»ÀœÚ»´–£Õ¨—ß◊˜∂¡ È–ƒµ√±®∏Ê£¨«Î”√ª≠ ˜◊¥ÕºªÚ¡–±Ì∑®«Û≥È»°µƒ¡Ω√˚—ß…˙∏’∫√ «1√˚ƒ–…˙∫Õ1√˚≈Æ…˙µƒ∏≈¬ £Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀÊ◊≈–≈œ¢ºº ıµƒ—∏√Õ∑¢’𣨻À√«»•…Ã≥°π∫ŒÔµƒ÷ß∏∂∑Ω Ω∏¸º”∂ý—˘°¢±„Ωð£Æƒ≥–£ ˝—ß–À»§–°◊ȅ˺∆¡À“ª∑ðµ˜≤ÈŒ æÌ£¨“™«Û√ø»À—°«“÷ª—°“ª÷÷ƒ„◊Óœ≤ª∂µƒ÷ß∏∂∑Ω Ω£Æœ÷Ω´µ˜≤ÈΩ·π˚Ω¯––Õ≥º∆≤¢ªÊ÷∆≥…»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨«ÎΩ·∫œÕº÷–À˘∏¯µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
£®1£©’‚¥ŒªÓ∂Øπ≤µ˜≤È¡À°° °°»À£ª‘⁄…»–ŒÕ≥º∆Õº÷–£¨±Ì æ°∞÷ß∏∂±¶°±÷ß∏∂µƒ…»–Œ‘≤–ƒΩ«µƒ∂» ˝Œ™°° °°£ª
£®2£©Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£Æπ€≤Ï¥ÀÕº£¨÷ß∏∂∑Ω Ωµƒ°∞÷⁄ ˝°± «°∞°° °°°±£ª
£®3£©‘⁄“ª¥Œπ∫ŒÔ÷–£¨–°√˜∫Õ–°¡¡∂ºœÎ¥”°∞Œ¢–≈°±°¢°∞÷ß∏∂±¶°±°¢°∞“¯––ø®°±»˝÷÷÷ß∏∂∑Ω Ω÷–—°“ª÷÷∑Ω ΩΩ¯––÷ß∏∂£¨«Î”√ª≠ ˜◊¥ÕºªÚ¡–±Ì∏Òµƒ∑Ω∑®£¨«Û≥ˆ¡Ω»À«°∫√—°‘ÒÕ¨“ª÷÷÷ß∏∂∑Ω Ωµƒ∏≈¬ £Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À∑·∏ª–£‘∞ŒƒªØ…˙ªÓ£¨Ã·∏þ—ß…˙µƒ◊€∫œÀÿ÷ £¨¥ŸΩ¯÷–—ß…˙»´√Ê∑¢’π£¨—ß–£ø™’π¡À∂ý÷÷…ÁÕ≈ªÓ∂أƖ°√˜œ≤ª∂µƒ…ÁÕ≈”–£∫∫œ≥™…ÁÕ≈°¢◊„«Ú…ÁÕ≈°¢ È∑®…ÁÕ≈°¢ø∆ºº…ÁÕ≈£®∑÷±”√◊÷ƒ∏A£¨B£¨C£¨D“¿¥Œ±Ì æ’‚Àƒ∏ˆ…ÁÕ≈£©£¨≤¢∞—’‚Àƒ∏ˆ◊÷ƒ∏∑÷±–¥‘⁄Àƒ’≈ÕÍ»´œýÕ¨µƒ≤ªÕ∏√˜µƒø®∆¨µƒ’˝√Ê…œ£¨»ª∫ÛΩ´’‚Àƒ’≈ø®∆¨±≥√Ê≥Ø…œœ¥‘»∫Û∑≈‘⁄◊¿√Ê…œ£Æ
£®1£©–°√˜¥”÷–Àʪ˙≥È»°“ª’≈ø®∆¨ «◊„«Ú…ÁÕ≈Bµƒ∏≈¬ «°° °°£Æ
£®2£©–°√˜œ»¥”÷–Àʪ˙≥È»°“ª’≈ø®∆¨£¨º«¬ºœ¬ø®∆¨…œµƒ◊÷ƒ∏∫Û≤ª∑≈ªÿ£¨‘Ÿ¥” £”ýµƒø®∆¨÷–Àʪ˙≥È»°“ª’≈ø®∆¨£¨º«¬ºœ¬ø®∆¨…œµƒ◊÷ƒ∏£Æ«Îƒ„”√¡–±Ì∑®ªÚª≠ ˜◊¥Õº∑®«Û≥ˆ–°√˜¡Ω¥Œ≥È»°µƒø®∆¨÷–”–“ª’≈ «ø∆ºº…ÁÕ≈Dµƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
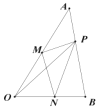
°æƒø°ø“—÷™»ÁÕº£¨![]() ÷–£¨
÷–£¨![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() …œ£¨
…œ£¨![]() £¨µ„
£¨µ„![]() °¢
°¢![]() ∑÷±‘⁄±þ
∑÷±‘⁄±þ![]() °¢
°¢![]() …œ“∆∂Ø£¨‘Ú
…œ“∆∂Ø£¨‘Ú![]() µƒ÷Ð≥§µƒ◊Ó–°÷µ «__________£Æ
µƒ÷Ð≥§µƒ◊Ó–°÷µ «__________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“ª¥Œ∫Ø ˝y=mx+n(m°Ÿ0)µƒÕºœÛ”Î∑¥±»¿˝∫Ø ˝y![]() (k°Ÿ0)µƒÕºœÛΩª”⁄µ⁄“ª°¢»˝œÛœÞƒ⁄µƒA°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨π˝µ„B◊˜BM°Õx÷·£¨¥π◊„Œ™µ„M£¨BM=OM=2£¨µ„Aµƒ◊ð◊¯±ÍŒ™4£Æ
(k°Ÿ0)µƒÕºœÛΩª”⁄µ⁄“ª°¢»˝œÛœÞƒ⁄µƒA°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨π˝µ„B◊˜BM°Õx÷·£¨¥π◊„Œ™µ„M£¨BM=OM=2£¨µ„Aµƒ◊ð◊¯±ÍŒ™4£Æ
£®1£©«Û∏√∑¥±»¿˝∫Ø ˝∫Õ“ª¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
£®2£©∏˘æðÕºœÛ÷±Ω”–¥≥ˆµ±mx+n![]() ±£¨xµƒ»°÷µ∑∂Œß£ª
±£¨xµƒ»°÷µ∑∂Œß£ª
£®3£©÷±œþABΩªx÷·”⁄µ„D£¨π˝µ„D◊˜÷±œþl°Õx÷·£¨»Áπ˚÷±œþl…œ¥Ê‘⁄µ„P£¨◊¯±Í∆Ω√ʃ⁄¥Ê‘⁄µ„Q£¨ π“‘O°¢P°¢A°¢QŒ™∂•µ„µƒÀƒ±þ–Œ «æÿ–Œ£¨÷±Ω”–¥≥ˆµ„Pµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
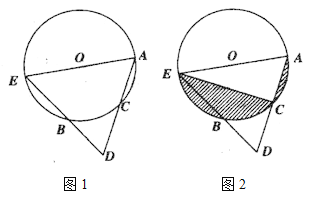
°æƒø°ø»ÁÕº1£¨‘⁄°—O÷–£¨µ„CŒ™¡”ª°ABµƒ÷–µ„£¨¡¨Ω”AC≤¢—”≥§÷¡D£¨ πCA=CD£¨¡¨Ω”DB≤¢—”≥§Ωª°—O”⁄µ„E£¨¡¨Ω”AE.
£®1£©«Û÷§£∫AE «°—Oµƒ÷±æ∂£ª
£®2£©»ÁÕº2£¨¡¨Ω”CE£¨°—Oµƒ∞Îæ∂Œ™5£¨AC≥§Œ™4£¨«Û“ı”∞≤ø∑÷√ʪ˝÷Æ∫Õ.(±£¡Ù![]() ”Î∏˘∫≈) .
”Î∏˘∫≈) .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com