
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= ;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
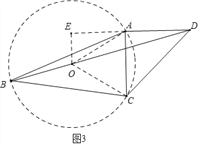
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.

【答案】(1)45°;(2)BD=5.(3)最大值为OB+OD=2+![]() +
+![]() .
.
【解析】分析:(1)由AC=AD得∠D=∠ACD,由平行四边形的性质得∠D=∠ABC,在△ACD中,由内角和定理求解;
(2)如图2,在△ABC外作等边△BAE,连接CE,利用旋转法证明△EAC≌△BAD,可证∠EBC=90°,BE=AB=3,在Rt△BCE中,由勾股定理求CE,由三角形全等得BD=CE;
(3)在△ACD的外部作等边三角形△ACO,以O为圆心OA为半径作⊙O,点B在⊙O上运动,作OE⊥DA交DA的延长线于E,构造直角三角形,根据勾股定理求解即可.
详解:(1)解:(1)如图1中,

∵AD∥BC,
∴∠DAC=∠BCA.∠DAB+∠ABC=180°.
∵AC=BC,
∴∠ABC=∠BAC.
∵∠DAC=2∠ABC,
∴2∠ABC+2∠ABC=180°,
∴∠ABC=45°
故答案为:45°;
(2)如图2,以AB为边在△ABC外作等边三角形△ABE,连接CE.

∵△ACD是等边三角形,
∴AD=AC,∠DAC=60°.
∵∠BAE=60°,
∴∠DAC+∠BAC=∠BAE+∠BAC.
即∠EAC=∠BAD
∴△EAC≌△BAD.
∴EC=BD.
∵∠BAE=60°,AE=AB=3,
∴△AEB是等边三角形,
∴∠EBA=60°,EB=3,
∵∠ABC=30°,
∴∠EBC=90°.
∵∠EBC=90°,EB=3,BC=4,
∴EC=5.
∴BD=5.
(3)如图3中,在△ACD的外部作等边三角形△ACO,以O为圆心OA为半径作⊙O.
∵∠ABC=![]() ∠AOC=30°,
∠AOC=30°,
∴点B在⊙O上运动,
作OE⊥DA交DA的延长线于E.
在Rt△AOE中,OA=AC=2,∠EAO=30°,
∴OE=![]() OA=1,AE=
OA=1,AE=![]() ,
,
在Rt△ODE中,DE=AE+AD=2+![]() ,
,
∴DO=![]() =
=![]() +
+![]() ,
,
当B、O、D共线时,BD的值最大,最大值为OB+OD=2+![]() +
+![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:点C是直线AB上一点,AC=6cm,BC=4cm,点M、N分别是AC、BC的中点;
(1)如图,点C在线段AB上,求线段MN的长;
(2)若点C在线段AB的延长线上,其他条件不变,则线段MN的长为_______cm.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,同学们利用如图所示的程序进行计算,计算按箭头指向循环进行.
如,当初始输入5时,即![]() =5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…
=5,第1次计算结果为16,第2次计算结果为8,第3次计算结果为4,…

(1)当初始输入1时,第1次计算结果为 ;
(2)当初始输入4时,第3次计算结果为 ;
(3)当初始输入3时,依次计算得到的所有结果中,有 个不同的值,第20次计算结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
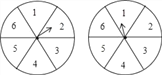
【题目】现有一项资助贫困生的公益活动由你来主持,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为12,则获得一等奖,奖金20元;数字之和为9,则获得二等奖,奖金10元;数字之和为7,则获得三等奖,奖金为5元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,活动结束后至少有多少赞助费用于资助贫困生?
查看答案和解析>>
科目:初中数学 来源: 题型:
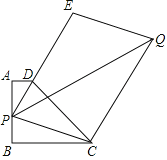
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=3,BC=4.若P为线段AB上任意一点,延长PD到E,使DE=2PD,再以PE、PC为边作平行四边形PCQE,求对角线PQ的最小值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌周围有20个箱子,按顺时针方向编号1~20,小明先在1号箱子中丢入一颗红球,然后沿着圆桌按顺时针方向行走,每经过一个箱子丢一颗球,规则如下

①若前一个箱子丢红球,则下一个箱子就丢绿球.
②若前一个箱子丢绿球,则下一个箱子就丢白球.
③若前一个箱子丢白球,则下一个箱子就丢红球.他沿着圆周走了2020圈,求4号箱内有_____颗红球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师计划组织朋友去晋西北游览两日,经了解,现有甲、乙两家旅行社比较合适,报价均为每人![]() 元,且提供的服务完全相同.针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过
元,且提供的服务完全相同.针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过![]() 人,每人都按九折收费,若超过
人,每人都按九折收费,若超过![]() 人,则其中
人,则其中![]() 人按九折收费,超出人数每人按七五折收费.假设组团参加两日游的人数为
人按九折收费,超出人数每人按七五折收费.假设组团参加两日游的人数为![]() 人.
人.
(1)请分别列式表示甲、乙两家旅行社收取组团两日游的总费用;
(2)若王老师组团参加两日游的人数共有![]() 人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com