
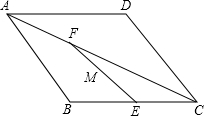
 在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒.
在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒. 分析 连接BD,DE交AC于F,先证明M从E到A所需时间的最小值是DE的长,然后求出DE即可解决问题.
解答 解:连接BD,DE交AC于F,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,
∵∠ABC=120°,
∴∠BCD=180°-∠ABC=60°,
∴△DBC是等边三角形,
∴DB=DC,
∵BE=EC,
∴ED⊥BC,
∴∠DEC=90°,
∴∠CDE=30°,
∴∠ADF=∠ADC-∠CDE=90°,
∵∠BAD=60°,
∴∠DAF=30°,
∴AF=2DF,
∴点M从E到A所需时间t=$\frac{EF}{1}$+$\frac{AF}{2}$=EF+DF=ED,此时M从E到A所需时间的最小,
这个最小值=DE=$\frac{\sqrt{3}}{2}$BC=3$\sqrt{3}$.
故答案为3$\sqrt{3}$.
点评 本题考查菱形的性质、最小值问题、垂线段最短等知识,解题的关键是添加辅助线,利用垂线段最短解决最小值问题,属于中考常考题型.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (a+b)2=a2+b2 | C. | (-a)3=-6a3 | D. | -(x-2)=2-x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
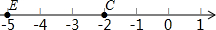 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )| A. | 26 | B. | 27 | C. | 28 | D. | 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a4÷a2=a2 | B. | (a+b)(a+b)=a2+b2 | C. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ | D. | (-$\frac{1}{2}$)-2=-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )
某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )| A. | 16,15 | B. | 15,15.5 | C. | 15,17 | D. | 15,16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com