
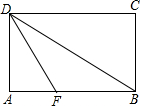
 如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°.
如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落在BD的中点处,则∠ADF=30°. 分析 由折叠可得∠DOF=∠A=90°,∠ADF=∠ODF,再根据FO垂直平分BD,可得∠FBO=∠FDO,进而得到∠FBO=∠FDO=∠ADF,据此可得∠ADF的度数.
解答 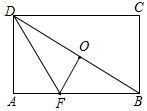 解:如图所示,由折叠可得∠DOF=∠A=90°,∠ADF=∠ODF,
解:如图所示,由折叠可得∠DOF=∠A=90°,∠ADF=∠ODF,
∵O是BD的中点,
∴FO垂直平分BD,
∴FB=FD,
∴∠FBO=∠FDO,
∴∠FBO=∠FDO=∠ADF,
又∵Rt△ABD中,∠FBO+∠FDO+∠ADF=90°,
∴∠ADF=30°,
故答案为:30°.
点评 本题主要考查了折叠问题以及三角形内角和定理的运用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
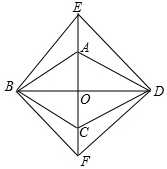 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD,AB=3,BC=4,点P是边AD的上一点,将△ABP沿着直线BP翻折,点A的对应点为点A′.若点A′到B点的距离等于它到CD边的距离,则AP=9-6$\sqrt{2}$.
如图,已知矩形ABCD,AB=3,BC=4,点P是边AD的上一点,将△ABP沿着直线BP翻折,点A的对应点为点A′.若点A′到B点的距离等于它到CD边的距离,则AP=9-6$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是( )
如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2017次后,顶点A在整个旋转过程中所经过的路程之和是( )| A. | 3022.5π | B. | 3024π | C. | 3025.5π | D. | 3026π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
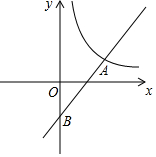 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(6,1),与y轴交于点B(0,-2)
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(6,1),与y轴交于点B(0,-2)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
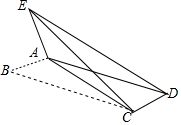 如图,在?ABCD中,AB<BC,已知∠B=30°,AB=2$\sqrt{3}$,将△ABC沿AC翻折至△AEC,使点B的对应点E落在?ABCD所在的平面内,连接ED,若△AED是直角三角形,则BC的长为4或6.
如图,在?ABCD中,AB<BC,已知∠B=30°,AB=2$\sqrt{3}$,将△ABC沿AC翻折至△AEC,使点B的对应点E落在?ABCD所在的平面内,连接ED,若△AED是直角三角形,则BC的长为4或6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
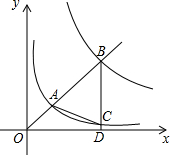 如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.
如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
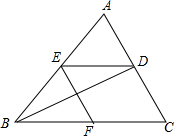 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.
如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,BE=CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com