
如图中几何体从正面看得到的平面图形是( )

A. 
B. 
C. 
D. 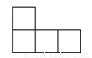
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米).
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1∶0.25.为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1∶1.75.施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备.工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan 31°≈0.60,sin 31°≈0.52)

查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
计算正确的是( )
A.  B.
B. 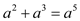 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型:单选题
用平面去截如图所示的三棱柱,截面形状不可能是( )

A. 三角形 B. 四边形 C. 五边形 D. 六边形
D 【解析】【解析】 用平面去截如图所示的三棱柱,截面形状可能是三角形、四边形、五边形,不可能是六边形.故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型:单选题
如图,在下面四个物体中,最接近圆柱的是( )



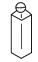
A. 烟囱 B. 弯管 C. 玩具硬币 D. 某种饮料瓶
C 【解析】【解析】 最接近圆柱的是玩具硬币.故选C.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
(本题满分10分)小明在一次高尔夫球的练习中,在点O处击球,其飞行路线满足抛物线 ,其中y(m)是球的飞行高度,
,其中y(m)是球的飞行高度,  (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.

(1)求抛物线的顶点坐标及球飞行的最大水平距离;
(2)若小明第二次仍从点O处击球,球飞行的最大高度不变且刚好进洞,求球飞行的抛物线路线满足的函数表达式.
(1)8m;(2)或 【解析】试题分析:(1)将抛物线配方化顶点式,可求出顶点坐标;令y=0,解方程可求出球飞行的组大水平距离. (2)根据飞行高度不变可得抛物线的顶点坐标,设出顶点式,进而把原点坐标代入即可求得相应的解析式. 【解析】 (1)∵=-, ∴抛物线顶点坐标为(4,4). 解得:x1=0,x2=8, ∴球飞行的最大水平距离为8m. (2)∵最...查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,△ABC是边长为12的等边三角形,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E的运动过程中,DF的最小值是______.

查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:单选题
方程 的解是( )
的解是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城市八年级(上)期末数学试卷(五四学制) 题型:填空题
如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=__度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com