
【题目】如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M,N分别在l1、l2上,点M,N,P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β. 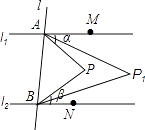
(1)当点P在l1与l2之间时. 求∠APB的大小(用含α、β的代数式表示);
(2)若∠APM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)
(3)当点P不在l1与l2之间时. 若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应的密文为a+b,b+c,c+d,d+2a.例如:明文1,2,3,4对应的密文为3,5,7,6.当接收方收到密文8,11,15,15时,则解密得到的明文应为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由. 已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2()
∵AC∥DE(已知)
∴∠1=∠3()
故∠2=∠3()
∵DF∥AE(已知)
∴∠2=∠5()
∴∠3=∠4()
∴DE平分∠BDE()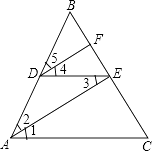
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图: 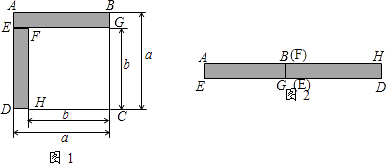
(1)如图1,已知正方形ABCD的边长为a,正方形FGCH的边长为b,长方形ABGE和EFHD为阴影部分,则阴影部分的面积是(写成平方差的形式)
(2)将图1中的长方形ABGE和EFHD剪下来,拼成图2所示的长方形,则长方形AHDE的面积是(写成多项式相乘的形式)
(3)比较图1与图2的阴影部分的面积,可得乘法公式 .
(4)利用所得公式计算:2(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )+
)+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com