

 ,求
,求 的值.
的值.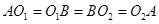 ,即可证得结论;(2)根据菱形的性质可得∠
,即可证得结论;(2)根据菱形的性质可得∠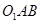 =∠
=∠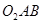 ,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠
,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠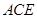 =∠
=∠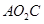 =90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;(3)
=90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;(3)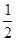
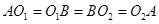 ,即可证得结论;
,即可证得结论;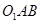 =∠
=∠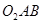 ,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠
,根据CE是⊙O1的切线,AC是⊙O1的直径可得∠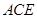 =∠
=∠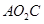 =90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;
=90°,即可证得△ACE∽△AO2D,根据相似三角形的性质求解即可;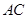 ∥
∥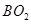 ,即可证得△ACD∽△
,即可证得△ACD∽△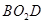 ,再根据相似三角形的性质及
,再根据相似三角形的性质及 求解即可.
求解即可.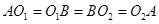
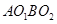 是菱形;
是菱形;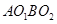 是菱形
是菱形 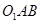 =∠
=∠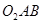
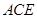 =∠
=∠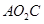 =90°
=90°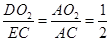 ,即
,即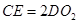 ;
;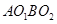 是菱形
是菱形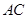 ∥
∥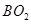
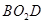
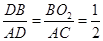
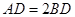
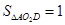
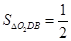 .
. 

 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源:不详 题型:解答题
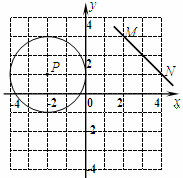
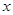 轴上截得的线段长度;
轴上截得的线段长度;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
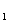 和⊙O
和⊙O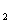 相切,两圆的圆心距为9cm,⊙
相切,两圆的圆心距为9cm,⊙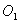 的半径为4cm,则⊙O
的半径为4cm,则⊙O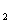 的半径为( )
的半径为( )| A.5cm | B.13cm | C.9 cm 或13cm | D.5cm 或13cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com