
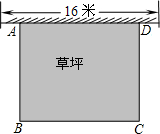
 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏利用一面墙如图围成一个矩形草坪ABCD.设该矩形草坪AB边的长为x米,面积为y平方米.
如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏利用一面墙如图围成一个矩形草坪ABCD.设该矩形草坪AB边的长为x米,面积为y平方米.分析 (1)利用矩形的面积计算公式得出y与x的函数关系式即可;
(2)利用(1)列出一元二次方程求解;
(3)利用(1)建立一元二次方程,由根的判别式就可以求出结论.
解答 解:(1)AB长为xm,则BC为(32-2x)m,
由题意得y=x(32-2x)=-2x2+32x(0<x≤8);
(2)由题意得 x(32-2x)=120,
解得x=6或x=10,
当x=6时,32-2x=20>16,不合题意,舍去,
当x=10时,32-2x=12<16,符合题意.
答:该矩形草坪BC边的长为12米;
(3)由题意得 x(32-2x)=140
∴x2-16x+70=0,
∴△=(-16)2-4×1×70=-240<0,
∴此方程无实数根,
∴不能围成面积是140平方米的矩形草坪ABCD.
点评 本题考查了一元二次方程的应用,表示出矩形草坪的长和宽,利用矩形的面积建立关系式与方程是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,正方形的边长为a,其中半径为r的圆是正方形内最大的圆,设阴影部分的面积为S.
如图,正方形的边长为a,其中半径为r的圆是正方形内最大的圆,设阴影部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 两张全等的直角三角形纸片△ABC和△DEF按如图所示摆放,点B、F、C、D在同一直线上,ED分别交AC,AB于点M、P
两张全等的直角三角形纸片△ABC和△DEF按如图所示摆放,点B、F、C、D在同一直线上,ED分别交AC,AB于点M、P查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于F.
如图,点P是菱形ABCD对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com