
【题目】若时钟由2点30分走到2点55分,问时针、分针各转过多大的角度?
科目:初中数学 来源: 题型:
【题目】定义:如图(1),若分别以△ABC的三边AC,BC,AB为边向三角形外侧作正方形ACDE,BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展双叶正方形. 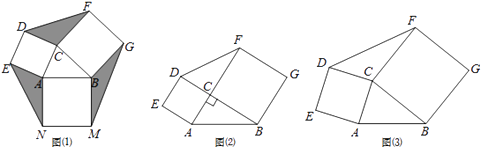
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为S1和S2 . ①如图(2),当∠ACB=90°时,求证:S1=S2 .
②如图(3),当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF,△AEN,△BGM的面积和为S,请利用图(1)探究:当∠ACB的度数发生变化时,S的值是否发生变化?若不变,求出S的值;若变化,求出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
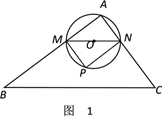
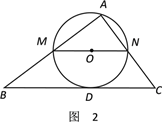
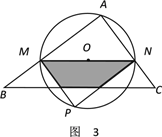
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=120°,OC在它的内部,且把∠AOB分成1:3的两个角,那么∠AOC的度数为( )
A.40°
B.40°或80°
C.30°
D.30°或90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com