
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¾ŲŠĪOCDEµÄČżøö¶„µć·Ö±šŹĒC£Ø3£¬0£©£¬D£Ø3£¬4£©£¬E£Ø0£¬4£©.ŅŌAĪŖ¶„µćµÄÅ×ĪļĻß¹żµćC£¬ĒŅ¶Ō³ĘÖį![]() ½»xÖįÓŚµćB£¬Į¬½įEC£¬AC£¬µćP”¢QĪŖ¶Æµć£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė”£
½»xÖįÓŚµćB£¬Į¬½įEC£¬AC£¬µćP”¢QĪŖ¶Æµć£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė”£
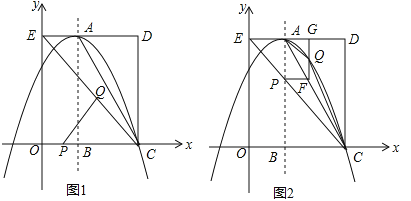
£Ø1£©Ö±½ÓŠ“³öAµć×ų±ź£¬²¢Ēó³öøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚĶ¼1ÖŠ£¬ČōµćPŌŚĻ߶ĪOCÉĻ“ÓµćOĻņµćCŅŌ1øöµ„Ī»/ĆėµÄĖŁ¶ČŌĖ¶Æ£¬Ķ¬Ź±µćQŌŚĻ߶ĪCEÉĻ“ÓµćCĻņµćEŅŌ2øöµ„Ī»/ĆėµÄĖŁ¶ČŌĖ¶Æ£¬µ±Ņ»øöµćµ½“ļÖÕµćŹ±£¬ĮķŅ»øöµćĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬µ±tĪŖŗĪÖµŹ±£¬![]() ĪŖÖ±½ĒČż½ĒŠĪ£æ
ĪŖÖ±½ĒČż½ĒŠĪ£æ
£Ø3£©ŌŚĶ¼2ÖŠ£¬ČōµćPŌŚ¶Ō³ĘÖįÉĻ“ÓµćBæŖŹ¼ĻņµćAŅŌ2øöµ„Ī»/ĆėµÄĖŁ¶ČŌĖ¶Æ£¬¹żµćP×÷![]() £¬½»ACÓŚµćF£¬¹żµćF×÷
£¬½»ACÓŚµćF£¬¹żµćF×÷![]() ÓŚµćG£¬½»Å×ĪļĻßÓŚµćQ£¬Į¬½įAQ£¬CQ.µ±tĪŖŗĪÖµŹ±£¬
ÓŚµćG£¬½»Å×ĪļĻßÓŚµćQ£¬Į¬½įAQ£¬CQ.µ±tĪŖŗĪÖµŹ±£¬![]() µÄĆ껿×ī“ó£æ×ī“óÖµŹĒ¶ąÉŁ£æ
µÄĆ껿×ī“ó£æ×ī“óÖµŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©AµÄ×ų±źĪŖ£Ø1£¬4£©£¬![]() £»£Ø2£©µ±
£»£Ø2£©µ±![]() »ņ
»ņ![]() Ź±£¬
Ź±£¬![]() ĪŖÖ±½ĒČż½ĒŠĪ£»£Ø3£©µ±
ĪŖÖ±½ĒČż½ĒŠĪ£»£Ø3£©µ±![]() Ź±£¬
Ź±£¬![]() µÄĆ껿×ī“ó£¬×ī“óÖµĪŖ1.
µÄĆ껿×ī“ó£¬×ī“óÖµĪŖ1.
”¾½āĪö”æ
£Ø1£©ÓɾŲŠĪµÄŠŌÖŹæÉÖ±½ÓĒóµĆAµć×ų±ź£¬æÉÉ趄µćŹ½·½³Ģ£¬°ŃCµć×ų±ź“śČėæÉĒóµĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©øł¾ŻĢāŅā±ķŹ¾³öP£¬Qµć×ų±ź£¬ŌŁĄūÓĆ“ż¶ØĻµŹż·ØĒó³öPQĖłŌŚÖ±Ļß½āĪöŹ½£¬½ų¶ų½«Dµć“śČėĒó³ö“š°ø£»
£Ø3£©ĻČĒóµĆÖ±ĻßACµÄ½āĪöŹ½£¬æÉ·Ö±šÓĆt±ķŹ¾³öPµćŗĶQµćµÄ×ų±ź£¬“Ó¶ųæÉĒóµĆFQµÄ³¤£¬æÉÓĆt±ķŹ¾³ö”÷ACQµÄĆ껿£¬ŌŁøł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹæÉĒóµĆĘä×ī“óÖµ£®
½ā£ŗ£Ø1£©”ßÅ×ĪļĻߵĶŌ³ĘÖį![]() £¬¾ŲŠĪOCDEµÄČżøö¶„µć·Ö±šŹĒC£Ø3£¬0£©£¬D£Ø3£¬4£©£¬E£Ø0£¬4£©
£¬¾ŲŠĪOCDEµÄČżøö¶„µć·Ö±šŹĒC£Ø3£¬0£©£¬D£Ø3£¬4£©£¬E£Ø0£¬4£©
”ąµćAµÄ×ų±źĪŖ£Ø1£¬4£©
ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗ![]()
°ŃC£Ø3£¬0£©“śČėÅ×ĪļĻß½āĪöŹ½£¬æÉµĆ£ŗ![]()
½āµĆ£ŗ![]()
¹ŹÅ×ĪļĻߵĽāĪöŹ½ĪŖ£ŗ![]() £¬¼“
£¬¼“![]()
£Ø2£©ÓÉĢāŅāµĆ£ŗ![]() £¬
£¬![]()
”ą![]()
µ±![]() Ź±
Ź±
ӧ![]()
”ą![]() ½āµĆ£ŗ
½āµĆ£ŗ![]()
µ±![]() Ź±
Ź±
ӧ![]()
”ą![]() ½āµĆ£ŗ
½āµĆ£ŗ![]()
”ąµ±![]() »ņ
»ņ![]() Ź±£¬
Ź±£¬![]() ĪŖÖ±½ĒČż½ĒŠĪ
ĪŖÖ±½ĒČż½ĒŠĪ
£Ø3£©”ßA£Ø1£¬4£©£¬C£Ø3£¬0£©
ÉčÖ±ĻßACµÄ½āĪöŹ½ĪŖ£ŗ![]()
![]() ½āµĆ£ŗ
½āµĆ£ŗ![]()
¹ŹÖ±ĻßACµÄ½āĪöŹ½ĪŖ£ŗ![]()
”ßP£Ø1£¬![]() £©£¬½«
£©£¬½«![]() “śČė
“śČė![]() µĆ£¬
µĆ£¬![]()
”ąQµćµÄŗį×ų±źĪŖ£ŗ![]()
½«![]() “śČė
“śČė![]() ÖŠ£¬µĆ
ÖŠ£¬µĆ![]()
”ąQµćµÄׯ×ų±źĪŖ£ŗ![]()
”ą![]()
”ą![]()
![]()
¼“![]()
![]()
”ąµ±![]() Ź±£¬
Ź±£¬![]() µÄĆ껿×ī“ó£¬×ī“óÖµĪŖ1
µÄĆ껿×ī“ó£¬×ī“óÖµĪŖ1


 ÓäæģµÄŗ®¼ŁÄĻ¾©³ö°ęÉēĻµĮŠ“š°ø
ÓäæģµÄŗ®¼ŁÄĻ¾©³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
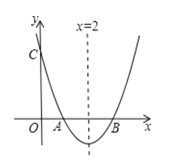
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½x2£«bx£«cÓėxÖį½»ÓŚµćA£¬B£¬AB£½2£¬ÓėyÖį½»ÓŚµćC£¬¶Ō³ĘÖįĪŖÖ±Ļßx£½2£®
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©øł¾ŻĶ¼Ļń£¬Ö±½ÓŠ“³ö²»µČŹ½x2£«bx£«c£¾0µÄ½ā¼Æ£ŗ £®
£Ø3£©ÉčDĪŖÅ×ĪļĻßÉĻŅ»µć£¬EĪŖ¶Ō³ĘÖįÉĻŅ»µć£¬ČōŅŌµćA£¬B£¬D£¬EĪŖ¶„µćµÄĖıߊĪŹĒĮāŠĪ£¬ŌņµćDµÄ×ų±źĪŖ£ŗ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ÓĆÅä·½·Ø½ā·½³Ģ£ŗx2-2x-2=0£»£Ø2£©ŅŃÖŖ¹ŲÓŚxµÄ·½³Ģ£Øm-2£©x2+£Øm-2£©x-1=0ÓŠĮ½øöĻąµČµÄŹµŹżøł£¬ĒómµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ü¼øÄź¹ŗĪļµÄÖ§ø¶·½Ź½ČÕŅęŌö¶ą£¬Ä³ŹżŃ§ŠĖȤŠ”×é¾Ķ“Ė½ųŠŠĮĖ³éŃłµ÷²é£®µ÷²é½į¹ūĻŌŹ¾£¬Ö§ø¶·½Ź½ÓŠ£ŗAĪ¢ŠÅ”¢BÖ§ø¶±¦”¢CĻÖ½š”¢DĘäĖū£¬øĆŠ”×é¶Ōij³¬ŹŠŅ»ĢģÄŚ¹ŗĀņÕßµÄÖ§ø¶·½Ź½½ųŠŠµ÷²éĶ³¼Ę£¬µĆµ½ČēĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£®

ĒėÄćøł¾ŻĶ³¼ĘĶ¼Ģį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±¾“ĪŅ»¹²µ÷²éĮĖ¶ąÉŁĆū¹ŗĀņÕߣæ
£Ø2£©Ēė²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠAÖÖÖ§ø¶·½Ź½Ėł¶ŌÓ¦µÄŌ²ŠÄ½ĒĪŖ”” ””¶Č£®
£Ø3£©ČōøĆ³¬ŹŠÕāŅ»ÖÜÄŚÓŠ1600Ćū¹ŗĀņÕߣ¬ĒėÄć¹Ą¼ĘŹ¹ÓĆAŗĶBĮ½ÖÖÖ§ø¶·½Ź½µÄ¹ŗĀņÕß¹²ÓŠ¶ąÉŁĆū£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
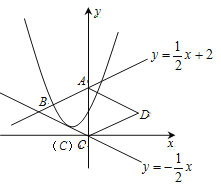
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļß![]() ÓėyÖį½»ÓŚµćA£¬ÓėÖ±Ļß
ÓėyÖį½»ÓŚµćA£¬ÓėÖ±Ļß![]() ½»ÓŚµćB£¬ŅŌABĪŖ±ßĻņÓŅ×öĮāŠĪABCD£¬µćCĒ”ÓėŌµćÖŲŗĻ£¬Å×ĪļĻß
½»ÓŚµćB£¬ŅŌABĪŖ±ßĻņÓŅ×öĮāŠĪABCD£¬µćCĒ”ÓėŌµćÖŲŗĻ£¬Å×ĪļĻß![]() µÄ¶„µćŌŚÖ±Ļß
µÄ¶„µćŌŚÖ±Ļß![]() ÉĻŅĘ¶Æ£¬ČōÅ×ĪļĻßÓėĮāŠĪµÄ±ßAB£¬BC¶¼ÓŠ¹«¹²µć£¬ŌņhµÄȔֵ·¶Ī§ŹĒ£Ø £©
ÉĻŅĘ¶Æ£¬ČōÅ×ĪļĻßÓėĮāŠĪµÄ±ßAB£¬BC¶¼ÓŠ¹«¹²µć£¬ŌņhµÄȔֵ·¶Ī§ŹĒ£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø4·Ö£©Ņ»ŌŖ¶ž“Ī·½³Ģ![]() µÄøłµÄĒéæöŹĒ£Ø £©
µÄøłµÄĒéæöŹĒ£Ø £©
A£®ÓŠĮ½øö²»ĻąµČµÄŹµŹżøł B£®ÓŠĮ½øöĻąµČµÄŹµŹżøł
C£®Ć»ÓŠŹµŹżøł D£®ĪŽ·ØČ·¶Ø
”¾“š°ø”æA£®
”¾½āĪö”æ
ŹŌĢā”ß”÷=![]() £¬”ą·½³ĢÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£®¹ŹŃ”A£®
£¬”ą·½³ĢÓŠĮ½øö²»ĻąµČµÄŹµŹżøł£®¹ŹŃ”A£®
æ¼µć£ŗøłµÄÅŠ±šŹ½£®
”¾ĢāŠĶ”æµ„Ń”Ģā
”¾½įŹų”æ
9
”¾ĢāÄæ”æŅŃÖŖÖ±Ļßy=kx£Øk£¾0£©ÓėĖ«ĒśĻß![]() ½»ÓŚµćA£Øx1£¬y1£©£¬B£Øx2£¬y2£©Į½µć£¬Ōņx1y2+x2y1µÄÖµĪŖ”¾ ”æ
½»ÓŚµćA£Øx1£¬y1£©£¬B£Øx2£¬y2£©Į½µć£¬Ōņx1y2+x2y1µÄÖµĪŖ”¾ ”æ
A£®©6 B£®©9 C£®0 D£®9
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬½«¾ŲŠĪABCDŃŲAFÕŪµž£¬Ź¹µćDĀäŌŚBC±ßµÄµćE“¦£¬¹żµćE×÷EG”ĪCD½»AFÓŚµćG£¬Į¬½ÓDG£®
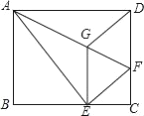
£Ø1£©ĒóÖ¤£ŗĖıߊĪEFDGŹĒĮāŠĪ£»
£Ø2£©ĒóÖ¤£ŗEG2=![]() GF”ĮAF£»
GF”ĮAF£»
£Ø3£©Čō![]() £¬ÕŪŗŪAF=5
£¬ÕŪŗŪAF=5![]() cm£¬Ōņ¾ŲŠĪABCDµÄÖܳ¤ĪŖ .
cm£¬Ōņ¾ŲŠĪABCDµÄÖܳ¤ĪŖ .
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£¬²¢½ā¾öĪŹĢā£ŗ
²ÄĮĻ1£ŗ¶ŌÓŚŅ»øöČżĪ»ŹżĘ䏮Ī»Źż×ÖµČÓŚøöĪ»Źż×ÖÓė°ŁĪ»Źż×ֵIJīµÄĮ½±¶£¬ŌņĪŅĆĒ³ĘÕāŃłµÄŹżĪŖ”°±¶²īŹż”±Čē122£¬![]() £»
£»
²ÄĮĻ2£ŗČōŅ»øöŹż![]() Äܹ»Š“³É
Äܹ»Š“³É![]() ¾łĪŖÕżÕūŹż£¬ĒŅ
¾łĪŖÕżÕūŹż£¬ĒŅ![]() £¬ŌņĪŅĆĒ³ĘÕāŃłµÄŹżĪŖ”°²»ĶźČ«Ę½·½²īŹż”±£¬
£¬ŌņĪŅĆĒ³ĘÕāŃłµÄŹżĪŖ”°²»ĶźČ«Ę½·½²īŹż”±£¬![]() ×ī“óŹ±£¬ĪŅĆĒ³Ę“ĖŹ±µÄ
×ī“óŹ±£¬ĪŅĆĒ³Ę“ĖŹ±µÄ![]() ”¢
”¢![]() ĪŖ
ĪŖ![]() µÄŅ»×é”°×īÓÅ·Ö½āŹż”±£¬¾®¹ę¶Ø
µÄŅ»×é”°×īÓÅ·Ö½āŹż”±£¬¾®¹ę¶Ø![]() £®ĄżČē
£®ĄżČē![]() £¬ŅņĪŖ£ŗ
£¬ŅņĪŖ£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]() £»
£»
£Ø1£©ĒóÖ¤£ŗČĪŅāµÄŅ»øö”°±¶²īŹż”±ÓėĘä°ŁĪ»Źż×ÖÖ®ŗĶÄܹ»±»3Õū³ż£»
£Ø2£©ČōŅ»øöŠ”ÓŚ300µÄČżĪ»Źż![]() ĘäÖŠ
ĘäÖŠ![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() ¾łĪŖÕūŹż£©¼ČŹĒŅ»øö”°²»ĶźČ«Ę½·½²īŹż”±£¬Ņ²ŹĒŅ»øö”°±¶²īŹż”±£¬ĒóĖłÓŠ
¾łĪŖÕūŹż£©¼ČŹĒŅ»øö”°²»ĶźČ«Ę½·½²īŹż”±£¬Ņ²ŹĒŅ»øö”°±¶²īŹż”±£¬ĒóĖłÓŠ![]() µÄ×ī“óÖµ£®
µÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬Óė
£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬µć
£¬µć![]() ŌŚ
ŌŚ![]() ÖįÕż°ėÖįÉĻ£¬
ÖįÕż°ėÖįÉĻ£¬![]() £®
£®
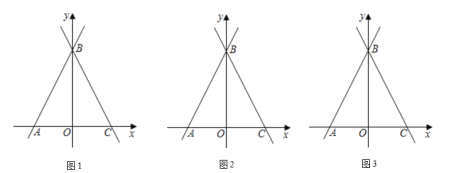
£Ø1£©ĒóÖ±Ļß![]() µÄ½āĪöŹ½£»
µÄ½āĪöŹ½£»
£Ø2£©µć![]() ŹĒÉäĻß
ŹĒÉäĻß![]() ÉĻŅ»µć£¬Į¬½Ó
ÉĻŅ»µć£¬Į¬½Ó![]() £¬Éčµć
£¬Éčµć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬
£¬![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]()
![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() µÄŗÆŹż½āĪöŹ½£¬²¢Ö±½ÓŠ“³ö×Ō±äĮæ
µÄŗÆŹż½āĪöŹ½£¬²¢Ö±½ÓŠ“³ö×Ō±äĮæ![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() µÄ“¹Ļߣ¬“¹×ćĪŖµć
µÄ“¹Ļߣ¬“¹×ćĪŖµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬½»Ļ߶Ī
£¬½»Ļ߶Ī![]() ÓŚµć
ÓŚµć![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ½»
½»![]() ÖįÓŚµć
ÖįÓŚµć![]() £¬µ±
£¬µ±![]() Ź±£¬ĒóÖ±Ļß
Ź±£¬ĒóÖ±Ļß![]() µÄ½āĪöŹ½£®
µÄ½āĪöŹ½£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com