
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系 ;
(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;
(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.
【答案】(1)∠A+∠C=90°;(2)∠C+∠BAD=90°,理由见解析;(3)99°.
【解析】
(1)根据平行线的性质以及直角三角形的性质进行证明即可;
(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C,可得∠C+∠BAD=90°;
(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+5α+(5α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=9°,进而得出∠EBC=∠ABE+∠ABC=9°+90°=99°.
(1)如图1,AM与BC的交点记作点O,
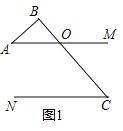
∵AM∥CN,
∴∠C=∠AOB,
∵AB⊥BC,
∴∠A+∠AOB=90°,
∴∠A+∠C=90°;
(2)如图2,过点B作BG∥DM,
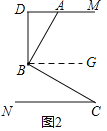
∵BD⊥AM,
∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,BG∥AM,
∴CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C,
∴∠C+∠BAD=90°;
(3)如图3,过点B作BG∥DM,
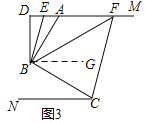
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(2)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=5∠DBE=5α,
∴∠AFC=5α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=5α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+5α+(5α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=9°,
∴∠ABE=9°,
∴∠EBC=∠ABE+∠ABC=9°+90°=99°.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】龙华区某学校开展“四点半课堂”,计划开设以下课外活动项目:![]() 版画、
版画、![]() 机器人、
机器人、![]() 航模、
航模、![]() 园艺种植
园艺种植![]() 为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查
为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查![]() 每位学生必须选且只能选其中一个项目
每位学生必须选且只能选其中一个项目![]() ,并将调查结果绘制成了如图1、2的两幅不完整的统计图,请根据图中的信息回答下列问题:
,并将调查结果绘制成了如图1、2的两幅不完整的统计图,请根据图中的信息回答下列问题:

![]() 这次被调查的学生共有______人;图1中,选“
这次被调查的学生共有______人;图1中,选“![]() 版画“所在扇形的圆心角度数为______
版画“所在扇形的圆心角度数为______![]() ;
;
![]() 请将图2的条形统计图补充完整;
请将图2的条形统计图补充完整;
![]() 若该校学生总人数为1500人,由于”
若该校学生总人数为1500人,由于”![]() 机器人“项目因故取消,原选“
机器人“项目因故取消,原选“![]() 机器人”中
机器人”中![]() 的学生转选了“
的学生转选了“![]() 航模”项目,则该校学生中选“
航模”项目,则该校学生中选“![]() 航模“项目的总人数为______人
航模“项目的总人数为______人![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示的是汽车在行驶的过程中,速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在那些时间段保持匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的![]() 倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长
倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长![]() 列方程
列方程![]() 组
组![]() 求解
求解![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”图中的P,Q两点即为“等距点”.

(1)已知点A的坐标为![]() .①在点
.①在点![]()
![]()
![]() 中,为点A的“等距点”的是________;②若点B的坐标为
中,为点A的“等距点”的是________;②若点B的坐标为![]() ,且A,B两点为“等距点”,则点B的坐标为________.
,且A,B两点为“等距点”,则点B的坐标为________.
(2)若![]()
![]() 两点为“等距点”,求k的值.
两点为“等距点”,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在等边△ABC的边BC上,BE=6,射线CD⊥BC于点C,点P是射线CD上一动点,点F是线段AB上一动点,当EP+PF的值最小时,BF=7,则AC为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
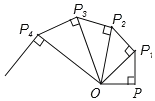
【题目】如图,OP=1,过P作PP1⊥OP,得OP1=![]() ;再过P1作P1P2⊥OP1且P1P2=1,得OP2=
;再过P1作P1P2⊥OP1且P1P2=1,得OP2=![]() ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,S1,S2,S3…分别表示各个三角形的面积,那么S12+S22+S32+…+S92的值是( )
;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2;…依次法继续作下去,S1,S2,S3…分别表示各个三角形的面积,那么S12+S22+S32+…+S92的值是( )
A.![]() B.
B.![]() C.
C.![]() D.55
D.55
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com