

分析 (1)根据旋转的性质即可得到结论;
(2)根据等边三角形的性质得到∠DAC=$\frac{1}{2}$∠BAC=30°,由三角形外角的性质的外角的性质即可得到结论.
(3)根据等边三角形的性质得到AD⊥BC,求得∠ADC=90°,得到∠A′DC=30°,推出∠A′=∠A′DC,根据平行线的判定定理即可得到结论.
解答 解:(1)∵把△ABD旋转n度,得到△A′B′D,
∴∠BDB′=∠ADA′=n°,
∵n=40,
∴∠ADA′=40°,
故答案为:40;
(2)∵△ABC是等边三角形,AD所在直线是它的对称轴,
∴∠DAC=$\frac{1}{2}$∠BAC=30°,
∴∠DEC=∠DAC+∠ADA′=30°+n°;
(3)当n=60时,A′B′∥DC,
∵△ABC是等边三角形,AD所在直线是它的对称轴,
∴AD⊥BC,
∴∠ADC=90°,
∵∠ADA′=60°,
∴∠A′DC=30°,
∵∠A′=∠DAC=30°,
∴∠A′=∠A′DC,
∴A′B′∥DC.
点评 本题考查了旋转的性质,等边三角形的性质,平行线的判定,熟练掌握旋转的性质是解题的关键.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | 点P(1,-3)在笫二象限 | B. | 已知点A(-3,4),点B(-3,2),则AB∥x轴 | ||
| C. | 点M(3,-2)到y轴的距离为2个单位 | D. | 已知点A(1,2),点B(-2.-1),则AB=3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
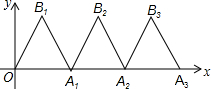 如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )
如图,将折线OB1A1记作f1,其中A1(4,0),OB1=A1B1.∠OB1A1=60°,依次将f1沿x轴正方向平移4个单位得f2,再将f2向右平移4个单位得f3…,若点P(23,n)在f6上,则n的值是( )| A. | 0 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 20 | C. | 40 | D. | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-3)2=9 | B. | |-3|=-3 | C. | $\sqrt{9}$=±3 | D. | $\root{3}{-64}$=-$\root{3}{64}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com