练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．在一个不透明的纸箱中有四张完全相同的卡片，上面分别画有圆、等腰直角三角形、平行四边形、等边三角形，从中随机抽取一张，卡片上的图形是中心对称图形的概率为$\frac{1}{2}$．

    分析 用中心对称图形的个数除以所有图形的个数即可求得答案．

    解答 解：在圆、等腰直角三角形、平行四边形、等边三角形四张卡片中，是中心对称图形的是：圆、平行四边形这2张，
    ∴卡片上的图形是中心对称图形的概率为$\frac{2}{4}$=$\frac{1}{2}$，
    故答案为：$\frac{1}{2}$．

    点评 本题考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

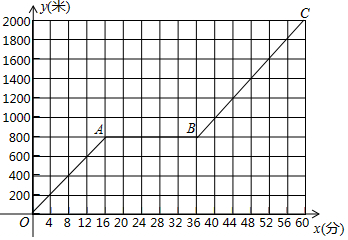    20．小明家到公园的路程为2000米，小明爸爸和小明先后从家出发步行去公园．爸爸先出发一直匀速前行，小明在爸爸走出200米后出发，途中他在休闲广场观棋停留一段时间．小明所走路程y（米）与步行时间x（分）的函数图象如图所所示．
    （1）求直线BC所对应的函数表达式．
    （2）在小明出发后的第20分钟，爸爸与小明第二次相遇，请在图中画出爸爸所走的路程y（米）与小明的步行时间x（分）的函数图象．
    （3）在速度都不变的情况下，小明希望比爸爸早8分钟到达公园，请直接写出小明怎样调整在休闲广场的观棋时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

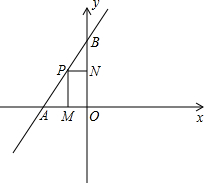    1．如图，在平面直角坐标系中，直线y=$\frac{3}{2}$x+6与x轴交于点A，与y轴交于点B，P为线段AB上一动点（不与A，B两点重合），过点P作PM⊥x轴，PN⊥y轴，垂足分别为M，N．设OM=a，四边形PMON面积为s．
    （1）A，B两点的坐标为（-4，0），（0，6），a的取值范围是0＜a＜4；
    （2）求s与a的函数表达式及s的最大值；
    （3）当s=$\frac{35}{6}$时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某市中学组织学生到距离学校6km的神舟科技馆去参观，学生李伟因事故耽误没能乘上学校的专车，于是准备在学校门口改乘出租车去神舟科技馆，出租车的收费标准如下：
     里程 收费
     2km以内（含2km） 10.0
     2km以上，每增加1km 1.40
    （1）写出出租车行驶的里程数x（x≥2km）与费用y（元）之间的函数关系式；
    （2）李伟同学身上仅有16元钱，乘出租车到科技馆的车费够不够？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知抛物线y=$\frac{1}{4}$（x-h）2交x轴，y轴的正半轴于A、B两点，且OA=2OB
    （1）求h的值；
    （2）平移直线AB交抛物线于M，交x轴于N，且$\frac{AB}{MN}$=$\frac{1}{4}$，求△MNO的面积；
    （3）点C为抛物线对称轴上顶点下方的一点，过点C作直线交抛物线于E、F，交x轴于D，探求$\frac{CD}{CE}$+$\frac{CD}{CF}$的值是否为定值？如果是请求出值；如果不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在平面直角坐标系xOy中，抛物线y=x2+bx+c经过点（0，-3），（2，-3）．
    （1）求抛物线的表达式；
    （2）求抛物线的顶点坐标及与x轴交点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，AB为⊙O的直径，CD与⊙O相切于点C，且OD⊥BC，垂足为F，OD交⊙O于点E．
    （1）证明：∠D=∠AEC；
    （2）证明：OA2=OD•OF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

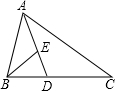    19．如图，△ABC中，D、E两点分别在BC、AD上，且AD平分∠BAC，若∠ABE=∠C，AD：ED=3：1，则△BDE与△ADC的面积比为（　　）
    A．16：45B．2：9C．1：9D．1：3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知：Rt△ABC斜边AB上点D，E，满足∠DCE=45°．
    （1）如图1，当AC=1，BC=$\sqrt{3}$，且点D与A重合时，求线段BE的长；
    （2）如图2，当△ABC是等腰直角三角形时，求证：AD2+BE2=DE2；
    （3）如图3，当AC=3，BC=4时，设AD=x，BE=y，求y关于x的函数关系式，并写出定义域．

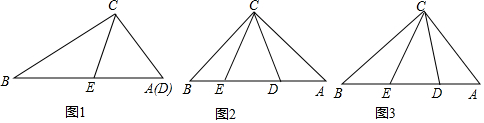
    查看答案和解析>>

    同步练习册答案