
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,AB=4,点
,AB=4,点![]() 是边
是边![]() 上动点(点
上动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() .
.

(1)求![]() 的大小;
的大小;
(2)若把![]() 沿着直线
沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
① 如图2,当点![]() 落在斜边
落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,![]() 与
与![]() 相交于点
相交于点![]() ,如果
,如果![]() ,写出
,写出![]() 与
与![]() 的函数关系式以及定义域.
的函数关系式以及定义域.
【答案】(1) ![]() ;(2) ①x=1,②
;(2) ①x=1,② ![]() ,定义域
,定义域![]()
【解析】
(1)根据正弦的定义求出∠B=30°,根据平行线的性质解答;
(2)根据翻转变换的性质,等边三角形的判定定理得到△AQP为等边三角形,根据等边三角形的性质得到AQ=QP,证明AQ=QC,计算即可;
(3)作QG⊥AB于G,RH⊥AB于H,根据正弦的定义用x表示出QG,证明RE=RB,根据等腰三角形的性质得到EH= ![]() y,根据正切的定义计算即可.
y,根据正切的定义计算即可.
解:(1) 在Rt△ABC中,
∵ ![]() ,AB=4,
,AB=4,
![]()
∴![]()
∵![]()
∴![]()
(2) ① 如图2,当点![]() 落在斜边
落在斜边![]() 上时;
上时;
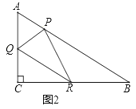
由翻折得![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
![]() 是等边三角形
是等边三角形
![]()
即x=1.
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,
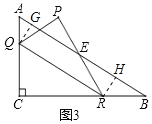
作QG⊥AB于G,
∵QR∥AB,
∴QG=RH,
在Rt△AQG中,QG=AQ×sinA![]()
由翻折的性质可知,∠PRP=∠CRQ=30°,
∵QR∥AB,
∴∠REB=∠PRQ,
∴∠REB=∠B,
∴RE=RB,
∵RH⊥AB,
![]()
在Rt△ERH中,![]()
∴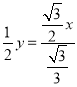
整理得,y=3x,
则y与x的函数关系式为y=3x(0<x<1).


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
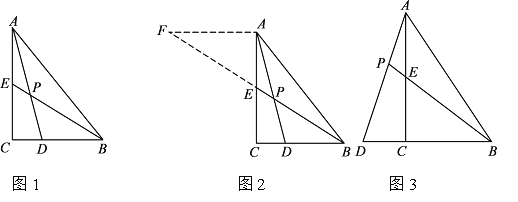
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,E 为 BC 边中点.
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD

(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
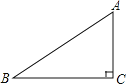
(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.
(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.

(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠ABC=45°,AD为△ABC的高,点E在边AC上,BE与AD交于点F,且DF=DC.
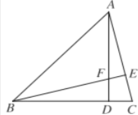
求证;(1)BF=AC;
(2)BE![]() AC.
AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸和妈妈上山游玩,爸爸步行,妈妈乘坐缆车,相约在山顶缆车的终点会合.已知爸爸步行的路程是缆车所经线路长的2.5倍,妈妈在爸爸出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折现反映了爸爸行走的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系.
(分钟)之间的函数关系.

(1)爸爸行走的总路程是 米,他途中休息了 分钟;
(2)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是 ;
之间的函数关系式是 ;
(3)爸爸休息之后行走的速度是每分钟 米;
(4)当妈妈到达缆车终点是,爸爸离缆车终点的路程是 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,
两点,
(1)求这两个函数表达式
(2)写出使反比例函数值大于一次函数值时![]() 的取值范围。
的取值范围。
(3)△AOB的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,![]() ).
).
(1)![]() _____,点A的坐标为______,点B的坐标为_____;
_____,点A的坐标为______,点B的坐标为_____;
(2)设抛物线![]() 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com