
 ����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H��
����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H��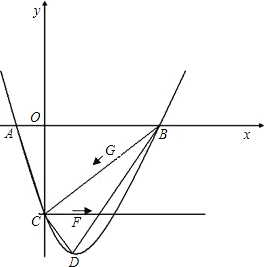 ���ꣻ�������ڣ���˵�����ɣ�
���ꣻ�������ڣ���˵�����ɣ� ��
�� ��BC=3
��BC=3 ��BD=2
��BD=2 ��
��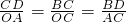 =
= ��
��
 t��OM=3-2
t��OM=3-2 t��
t�� t��-2
t��-2 t����
t���� t��
t�� t��-2
t��-2 t����H2��3-
t����H2��3- t��-2
t��-2 t����
t���� t��2-2��3-3
t��2-2��3-3 t��-3=-2
t��-3=-2 t��
t�� t=0��
t=0��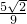 ��
��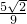 ʱ��H1��-
ʱ��H1��- ��-
��- ����
���� t��2-2��3-
t��2-2��3- t��-3=-2
t��-3=-2 t��
t�� t=0��
t=0�� ��
�� ʱ��H2��1��-4����
ʱ��H2��1��-4���� t-
t- t=3-3
t=3-3 t��CQ=CP=3-2
t��CQ=CP=3-2 t��
t�� t��
t�� t-3��2
t-3��2 t-6����
t-6���� t-3��2-2��3
t-3��2-2��3 t-3��-3=2
t-3��-3=2 t-6��
t-6�� t+9=0��
t+9=0��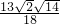 ��
��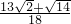 ʱ��H3��
ʱ��H3�� ��
��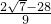 ����
����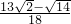 ʱ��H4��
ʱ��H4��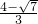 ��
�� ����
����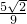 ʱ��H1��-
ʱ��H1��- ��-
��- ����
���� ʱ��H2��1��-4����
ʱ��H2��1��-4����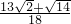 ʱ��H3��
ʱ��H3�� ��
��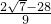 ����
����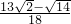 ʱ��H4��
ʱ��H4��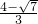 ��
�� ����
����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
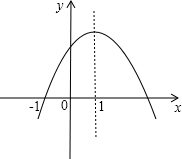 ��֪��ͼ������y=ax2+bx+c������ʽ�ӳ������ǣ�������
��֪��ͼ������y=ax2+bx+c������ʽ�ӳ������ǣ�������| A��a+b+c��0 | B��b��a+c | C��c��2b | D��abc��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
 ���ꣻ�������ڣ���˵�����ɣ�
���ꣻ�������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��l2������M�������Ծ�����A1B1�������������䣩����ô�����ܵ��ļ����������˻�����С�ˣ�˵�����ɣ�
��l2������M�������Ծ�����A1B1�������������䣩����ô�����ܵ��ļ����������˻�����С�ˣ�˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010�����ʡ�п���ѧģ���Ծ���10���������棩 ���ͣ������
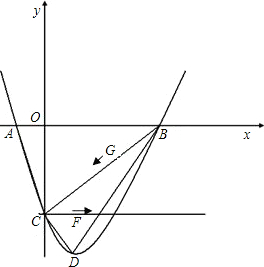
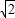 ����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H�����ꣻ�������ڣ���˵�����ɣ�
����λ���ٶ���CF����������CE���˶�������G��B�㿪ʼ��ÿ��4����λ�ٶ���BC����������BC���˶����趯��F��Gͬʱ�����˶�ʱ��Ϊt���������������Ƿ���ڵ�H��ʹ��C��G��H��F�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ������Ӧt��ֵ��H�����ꣻ�������ڣ���˵�����ɣ�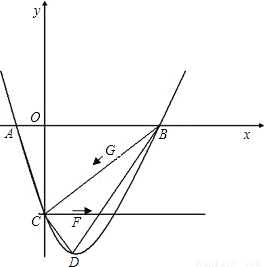
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com