
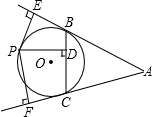
 于F.
于F.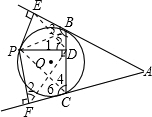 证明:
证明: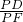 =
=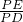 ,即PD2=PF•PE.
,即PD2=PF•PE.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
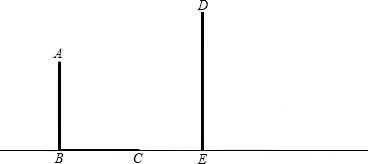 阳光下的投影长为6m,请你计算DE的长.
阳光下的投影长为6m,请你计算DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.查看答案和解析>>
科目:初中数学 来源: 题型:
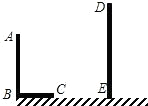
 已知,如图,AB和DE是直立在地面上的两根立柱.AB=7m,某一时刻AB在太阳光下的投影BC=4m.
已知,如图,AB和DE是直立在地面上的两根立柱.AB=7m,某一时刻AB在太阳光下的投影BC=4m.查看答案和解析>>
科目:初中数学 来源:2010-2011学年达州市高中阶段教育学校招生统一考试数学卷 题型:解答题
已知:如图,AB和DE是直立在地面上的两根立柱,AB="5" m,某一时刻,AB在阳光下的投影BC="4" m.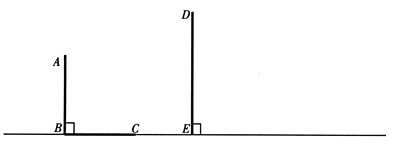
【小题1】请你在图中画出此时DE在阳光下的投影,并简述画图步骤;
【小题2】在测量AB的投影长时,同时测出DE在阳光下的投影长为6 m,请你计算DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com