
���� ��1�������A���꣬���������ߵĽ���ʽ�������c��ֵ��
��2���ѵ�B�������y=ax2+bx+c��ֱ��y=ax+n��$\left\{\begin{array}{l}{a��m-b��^{2}+b��m-b��-\frac{1}{2}={m}^{2}-mb-\frac{1}{2}}&{��}\\{{m}^{2}-mb-\frac{1}{2}=a��m-b��-\frac{1}{2}}&{��}\end{array}\right.$���ⷽ����ɵ�a=1�����ݸ���ϵ����ϵ���ɽ�����⣮
��3����������������ͼ������ɣ�
��� �⣺��1���ߵ�A��y�Ḻ���ᣬ��ƫ�����Ϊ$\frac{1}{2}$��
���A���꣨0��-$\frac{1}{2}$�����ֱ����y=ax2+bx+c��ֱ��y=ax+n�У��ɵ�c=n=-$\frac{1}{2}$��
��c=-$\frac{1}{2}$��
��2���ѵ�B�������y=ax2+bx+c��ֱ��y=ax+n��$\left\{\begin{array}{l}{a��m-b��^{2}+b��m-b��-\frac{1}{2}={m}^{2}-mb-\frac{1}{2}}&{��}\\{{m}^{2}-mb-\frac{1}{2}=a��m-b��-\frac{1}{2}}&{��}\end{array}\right.$
�ɢڵõ���m-b����m-a��=0��
��A��B�Dz�ͬ���㣬
��m-b��0��
��m=a��
��m=a����������õ���a-b��2��a-1��=0��
��m-b��0��
��m��b����m=a��
��a-b��0��
��a-1=0��
��a=1��
�������ߵĽ���ʽΪy=x2+bx-$\frac{1}{2}$��
��������y=ax2+bx+c��ƫ�����Ϊ0��������ĺ�����ֱ�Ϊx1��x2��
��x1��x2�Ƿ��̣�x2+bx-$\frac{1}{2}$=0��������
��x1•x2=-$\frac{1}{2}$��
��3���������ߵĽ���ʽΪy=x2+bx-$\frac{1}{2}$��
��y=x2+bx-$\frac{1}{2}$=��x+$\frac{b}{2}$��2-$\frac{{b}^{2}}{4}$-$\frac{1}{2}$��
��x=-1ʱ��y=$\frac{1}{2}$-b��
��x=1ʱ��y=$\frac{1}{2}$+b��
��y1=|-$\frac{{b}^{2}}{4}$-$\frac{1}{2}$|=$\frac{{b}^{2}}{4}+\frac{1}{2}$��
y2=|$\frac{1}{2}$-b|��
y3=|$\frac{1}{2}$+b|��
��ͬһ����ϵ�л�������ͼ����ͼ��ʾ��y2��y3��ͼ����ͬ����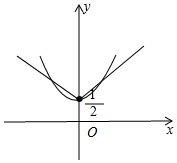
����ƫ�����Ķ��壬������y=ax2+bx+c��-1��x��1�ϵ����ƫ�����d����Сֵ���Ƕ���ͬһ�Ա���x������ֵy1/��y2��y3�н�С��ֵ��
��ͼ���֪��������y=ax2+bx+c��-1��x��1�ϵ����ƫ�����d����СֵΪ$\frac{1}{2}$��
���� ���⿼����κ����ۺ��⡢һ�κ���������ϵ������һԪ���η��̣�����ϵ����ϵ���������֪ʶ������Ĺؼ����������⣬ѧ�ṹ���������ʵ�����⣬�����п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
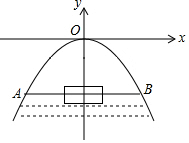 ��ͼ��һ�����߹��ţ�����O��ˮ���4�ף�ˮ�����AB=10�ף�����һ��������һֻ������������ͨ������֪���䳤10�ף���6�ף���2.5�ף�������ˮ���ƽ�����ʻ����ܷ�˳��ͨ�����ţ�
��ͼ��һ�����߹��ţ�����O��ˮ���4�ף�ˮ�����AB=10�ף�����һ��������һֻ������������ͨ������֪���䳤10�ף���6�ף���2.5�ף�������ˮ���ƽ�����ʻ����ܷ�˳��ͨ�����ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��n | B�� | m��n | C�� | m=n | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���������������й���ͳ��ѧ����Ҫ���������춨���й���ͳ��ѧ�Ļ�����ܣ����Ĵ����ɾ���Ҫ�������������������ͷ����������У��������ǡ�������������ߵ���ѧ�ɾͣ������������������ɡ�һ�¼��أ������л��߶��ڹ����߰˴磬������ȥ��һ�ɣ��ʻ��ߡ�������Σ���
���������������й���ͳ��ѧ����Ҫ���������춨���й���ͳ��ѧ�Ļ�����ܣ����Ĵ����ɾ���Ҫ�������������������ͷ����������У��������ǡ�������������ߵ���ѧ�ɾͣ������������������ɡ�һ�¼��أ������л��߶��ڹ����߰˴磬������ȥ��һ�ɣ��ʻ��ߡ�������Σ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
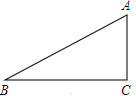 ��ͼ����֪��Rt��ABC�У���C=90�㣬3AC=2AB���ֱ����A�͡�B���ĸ�������Ǻ���ֵ��
��ͼ����֪��Rt��ABC�У���C=90�㣬3AC=2AB���ֱ����A�͡�B���ĸ�������Ǻ���ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
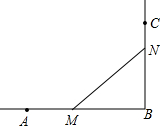 ��ͼ����֪AB��BC��AB=12cm��BC=8cm��һֻ���ӵ�C��CB������1cm/s���ٶ����У�һֻ���Ϊ�˲���ֻ�����ɵ�A��AB������2cm/s���ٶ����У�һ��ʱ������Ƿֱ��˵�M��N��λ�ã�����ʱ��MNB�����Ϊ24cm2�����������е�ʱ�䣮
��ͼ����֪AB��BC��AB=12cm��BC=8cm��һֻ���ӵ�C��CB������1cm/s���ٶ����У�һֻ���Ϊ�˲���ֻ�����ɵ�A��AB������2cm/s���ٶ����У�һ��ʱ������Ƿֱ��˵�M��N��λ�ã�����ʱ��MNB�����Ϊ24cm2�����������е�ʱ�䣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com