
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)去乙园采摘可以得到更多数量的草莓.
;(3)去乙园采摘可以得到更多数量的草莓.
【解析】
(1)根据表格数据,利用待定系数法由当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() 即可求解;
即可求解;
(2)设草莓在生长旺季前的销售价格为![]() 元/千克,根据在甲园、乙园采摘草莓
元/千克,根据在甲园、乙园采摘草莓![]() 时,所需费用相同列方程即可求出销售价格为
时,所需费用相同列方程即可求出销售价格为![]() 元/千克;依据收费规则直接可得
元/千克;依据收费规则直接可得![]() ;
;
(3)利用已求出函数解析式分别求出当花费![]() 元可得草莓数量进行比较即可解答.
元可得草莓数量进行比较即可解答.
解:(1)设![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
![]()
解得:![]()
![]() .
.
(2)设草莓在生长旺季前的销售价格为![]() 元/千克,根据题意,得:
元/千克,根据题意,得:
![]()
解得:![]() (元/千克).
(元/千克).
![]()
![]() .
.
![]() 答:去乙园采摘可以得到更多数量的草莓.
答:去乙园采摘可以得到更多数量的草莓.
当![]() 时,有:
时,有:![]() .
.
解得![]() ;
;
当![]() 时,
时,![]() ,
,
![]() ,
,
解得![]() ,
,
![]() .
.
![]() 去乙园采摘可以得到更多数量的草莓.
去乙园采摘可以得到更多数量的草莓.


科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象经过点
的图象经过点![]() (0,-4)和
(0,-4)和![]() (-2,2).
(-2,2).
(1)求![]() 的值,并用含
的值,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)求证:此抛物线与![]() 轴有两个不同交点;
轴有两个不同交点;
(3)当![]() 时,若二次函数满足
时,若二次函数满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围;
的取值范围;
(4) 直线![]() 上有一点
上有一点![]() (
(![]() ,5),将点
,5),将点![]() 向右平移4个单位长度,得到点
向右平移4个单位长度,得到点![]() ,若抛物线与线段
,若抛物线与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
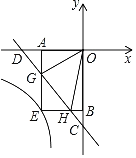
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=![]() 的解析式为_____.
的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
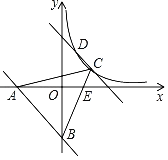
【题目】如图所示,一次函数y=﹣x﹣6与x轴,y轴分别交于点A,B将直线AB沿y轴正方向平移与反比例函数y=![]() (x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(1)求直线AC和反比例函数的解析式;
(2)连接AD,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
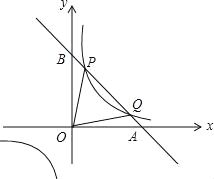
【题目】已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P(![]() ,n),Q(4,m)两点,且tan∠BOP=
,n),Q(4,m)两点,且tan∠BOP=![]() :
:
(1)求反比例函数和直线的函数表达式;
(2)求△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
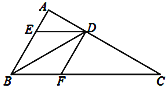
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
⑴求证:四边形BEDF为菱形;
⑵如果∠A=100°,∠C=30°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
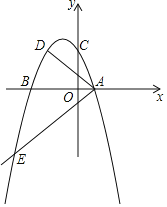
【题目】如图,二次函数y=a(x2+2mx﹣3m2)(其中a,m是常数a<0,m>0)的图象与x轴分别交于A、B(点A位于点B的右侧),与y轴交于点C(0,3),点D在二次函数的图象上,CD∥AB,连结AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)求a与m的关系式;
(2)求证:![]() 为定值;
为定值;
(3)设该二次函数的图象的顶点为F.探索:在x轴的正半轴上是否存在点G,连结GF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
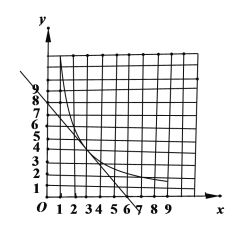
(1)填空:反比例函数的解析式为____________________,直线AC的解析式为____________________,B点的坐标是________.
(2)在平面内有点D,使得以A,B,C,D四点为项点的边形为平行四边形.
①在图中用直尺和2B铅笔画出所有符合条件的平行四边形;
②根据所画形,请直接写出符合条件的所有点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com