
如图1,在边长为5的正方形![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,且
边上的点,且![]() ,
,![]() .
.
(1)求![]() ∶
∶![]() 的值;
的值;
(2)延长![]() 交正方形外角平分线
交正方形外角平分线![]() (如图2),试判断
(如图2),试判断![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(3)在图2的![]() 边上是否存在一点
边上是否存在一点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,请给予证明;若不存在,请说明理由.
是平行四边形?若存在,请给予证明;若不存在,请说明理由.
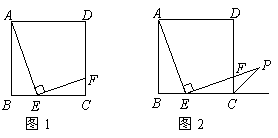 |
(1)解:∵AE⊥EF∴∠AEF=90º ∴∠AEB+∠CEF=90º
∵∠B=90º ∴∠BAE+∠AEB=90º
∴∠BAE=∠CEF ∵∠B=∠C
∴△ABE∽△ECF ∴AB/EC=BE/CF
∵AB=BC=5 BE=2 ∴EC=3
∴CF=6/5
∴EC/CF=5/2
(2)过P作PN⊥BC交与点N
∵FC∥PN ∴FC∶PN=EC∶EN
∵PC平分∠DCN ∴∠PCN=∠PNC=45º ∴CN=PN
∴PN=2=BE
∵∠1=∠PEN ∠B=∠ENP
∴△ABE≌△ENP ∴AE=EP
(3)解法:在![]() 边上存在一点
边上存在一点![]() ,使四边形
,使四边形![]() 是平行四边形
是平行四边形

证明:在![]() 边上取一点
边上取一点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
∴DM∥EP ∵AE=EP ∴DM=EP


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
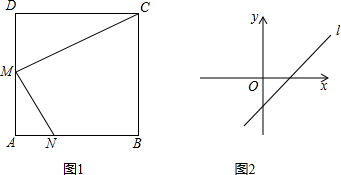
| n24n+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
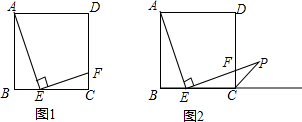
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
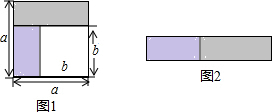
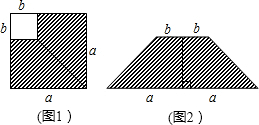 如图1,在边长为a的正方形中剪去一个边长为b的小正形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的乘法公式是
如图1,在边长为a的正方形中剪去一个边长为b的小正形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的乘法公式是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com