
【题目】如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10.点E是CD的中点,则AE的长为( )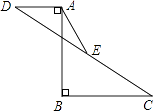
A.6
B.![]()
C.5
D.![]()
【答案】B
【解析】解:延长AE交BC于F,如图所示: 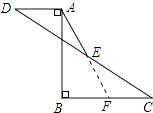
∵AB⊥BC,AB⊥AD,
∴AD∥BC,
∴∠D=∠C,
∵点E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,
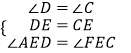 ,
,
∴△ADE≌△FCE(ASA),
∴AE=FE,AD=CF=5,
∴BF=BC﹣CF=5,
在Rt△ABF中,AF= ![]() =
= ![]() =13,
=13,
∴AE= ![]() AF=
AF= ![]() .
.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】李大伯承包了一片荒山,在山上种植了一部分优质油桃,今年已进入第三年收获期.今年收获油桃6 912千克,已知李大伯第一年收获的油桃重量为4 800千克.试求去年和今年两年油桃产量的年平均增长率,照此增长率,预计明年油桃的产量为多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )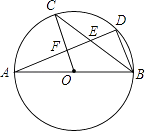
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小辉从家(点0)出发,沿着等腰三角形A0B的边0A-AB-B0的路径去匀匀速散步,其中0A=0B。设小辉距家(点0)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿直线AD折叠,点B与点E重合,连接BE交AD于O.∠ABC=90°,AB=6,BC=8,AC=10,SACD=15.有下列结论:①SCDE=5;②CD=5;③OB=OE;④SABD:SACD=3:4,则以上结论正确的是( )
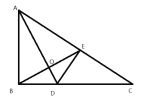
A. ①②B. ②③C. ②③④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
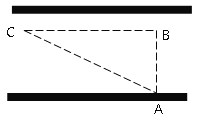
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AD平分∠BAC交BC于点D,点M,N分别是AD和AB上的动点,当SABC=6,AC=4时,BM+MN的最小值等于_______。
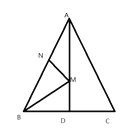
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,是一个长为 2m,宽为 2n 的长方形,沿图中虚线用剪刀将其均分成四个完全相同的小长方形,然后按图 2 的形状拼图.
(1)图 2 中的图形阴影部分的边长为 ;(用含 m、n 的代数式表示)
(2)请你用两种不同的方法分别求图 2 中阴影部分的面积; 方法一: ;方法二: .
(3)观察图 2,请写出代数式(m+n)2、(m﹣n)2、4mn 之间的关系式: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com