
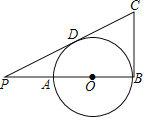
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
A.1.5B.2C.![]() D.
D.![]()
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】小李经营一个社区快递网点,负责周边快件收发,由于疫情原因,到2020年2月12 日网点才可以复工,而该网点的另外两名员工因为办理复工手续,将分别在2月15日和2月26日返岗,工作据大数据显示,预计从复工之日开始,每日到达该网点的快件数量![]() (件)与第
(件)与第![]() 天(2月12日为第
天(2月12日为第![]() 天)满足:
天)满足: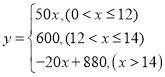 .已知一位快递员日均派送快件量为
.已知一位快递员日均派送快件量为![]() 件,通过加班最高可派送
件,通过加班最高可派送![]() 件.
件.
![]() 前三天小李派送的快件总量为_ 件;
前三天小李派送的快件总量为_ 件;
![]() 以最高派送量派送快件还有剩余时,则当天剩余快件留到第二天优先派送,
以最高派送量派送快件还有剩余时,则当天剩余快件留到第二天优先派送,
①到第十天结束时,滞留的快件共有 件; 到第十四天结束时,滞留的快件共有__件;
②2月18日后快递激增爆仓,小李和员工每天加班派送,根据现有快递数量的变化趋势,从2月19日开始计算,小李至少要加班几天才可以不用加班派送.(即小李不加班派送的情况下,快递点没有滞留件)
![]() 到了3月5日,全国疫情稳定,预计每日到达网点的快件数量将按新趋势变化,“女神节”期间(3月6日-9日)日均快件量为
到了3月5日,全国疫情稳定,预计每日到达网点的快件数量将按新趋势变化,“女神节”期间(3月6日-9日)日均快件量为![]() 件,3月10日起日均快件量稳定在
件,3月10日起日均快件量稳定在![]() 件.此时小李接到快递总公司新规定:从3月10日开始,到达的快件必须当天派送完毕,否则将扣除滞留快件滞留费
件.此时小李接到快递总公司新规定:从3月10日开始,到达的快件必须当天派送完毕,否则将扣除滞留快件滞留费![]() 元/件天(之前滞留的快件从3月10日0时开始收取滞留费)为此,小李想到从市场招聘____名临时工帮助派送快递,若临时工基本工资
元/件天(之前滞留的快件从3月10日0时开始收取滞留费)为此,小李想到从市场招聘____名临时工帮助派送快递,若临时工基本工资![]() 元/天,外加派送费
元/天,外加派送费![]() 元/件临时工一天最多可派送快件
元/件临时工一天最多可派送快件![]() 件,为了将支出降到最低,小李应该聘请临时工几天,派送快件共多少件?此时最低支出多少元钱?直接写出你的答案.
件,为了将支出降到最低,小李应该聘请临时工几天,派送快件共多少件?此时最低支出多少元钱?直接写出你的答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n).给出下列结论:①2a+c<0;②若(﹣![]() ,y1),(﹣
,y1),(﹣![]() ,y2),(
,y2),(![]() ,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣
,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n=﹣![]() 时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).
时,△ABP为等腰直角三角形.其中正确结论是______(填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A的坐标是A(x,y),从1、2、3这三个数中任取一个数作为x的值,再从余下的两个数中任取一个数作为y的值.则点A落在直线y=﹣x+5与直线y=![]() x及y轴所围成的封闭区域内(含边界)的概率是_____.
x及y轴所围成的封闭区域内(含边界)的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个两位数m,如果m等于两个正整数的平方和,那么称这个两位数m为“平方和数”,若m=a2+b2(a、b为正整数),记A(m)=ab.例如:29=22+52,29就是一个“平方和数”,则A(29)=2×5=10.
(1)判断25是否是“平方和数”,若是,请计算A(25)的值;若不是,请说明理由;
(2)若k是一个“平方和数”,且A(k)=![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.已知⊙M与x轴交于A、B两点,与y轴交于C、D两点,A、B两点的横坐标分别为﹣1和7,弦AB的弦心距MN为3,
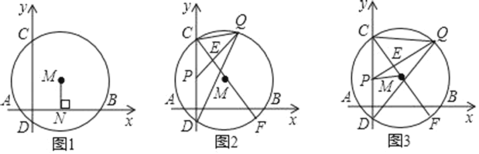
(1)求⊙M的半径;
(2)如图2,P在弦CD上,且CP=2,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,
①判断线段PQ与直径CF的位置关系,并说明理由;
②求CQ的长;
(3)如图3.若P点是弦CD上一动点,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ与∠CQD互余时,求△PEM面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校同安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
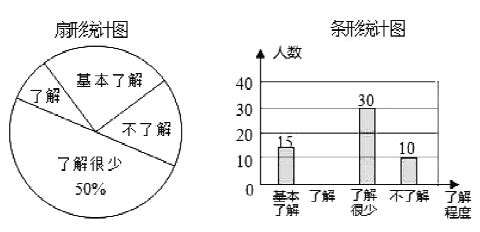
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 度;并补全条形统计图.
(2)若该中学共有学生![]() 人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的![]() 个女生
个女生![]() 和
和![]() 个男生
个男生![]() 中分别随机抽取
中分别随机抽取![]() 人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生
人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com