练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    求证：两条直线被第三条直线所截，如果同旁内角的角平分线互相垂直， 那么这两条直线互相平行．

    证明过程见试题解析．

    解析试题分析：两条直线被第三条直线所截，同旁内角的角平分线互相垂直，根据角平分线的性质求出这对同旁内角和的一半是90°，得到一对同旁内角的和是180°，所以两条直线平行．
    试题解析：如图，已知AB、CD被EF所截，EG、FG分别平分∠BEF、∠DFE，且EG⊥FG，求证：AB∥CD．

    证明：∵EG⊥FG，∴∠GEF+∠EFG=90°，∵EG、FG分别平分∠BEF、∠DFE，∴∠BEF+∠DFE=2(∠GEF+∠EFG)=180°，∴AB∥CD．
    考点：1．平行线的判定；2．角平分线的定义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    如图：BD平分∠ABC,F在AB上，G在AC上，FC与BD相交于点H.，
    求证： .

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知∠AOB， OE平分∠AOC， OF平分∠BOC.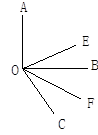

    （1）若∠AOB是直角，∠BOC=60°，求∠EOF的度数；
    （2）猜想∠EOF与∠AOB的数量关系；
    （3）若∠AOB+∠EOF＝156°，则∠EOF是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知：如图，是直角，，是的平分线，是的平分线．

    （1）求的大小.
    （2）当锐角的大小发生改变时，的大小是否发生改变？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    填写适当的理由：如图，已知：AB∥ED，你能求出∠B+∠BCD+∠D的大小吗？
    解：过点C画FC∥AB
    ∵AB∥ED（　　）
    FC∥AB（  ）
    ∴FC∥ED（　　）
    ∴∠B+∠1=180°
    ∠D+∠2=180°（　　）
    ∴∠B+∠1+∠D+∠2=　　°（    ）
    即：∠B+∠BCD+∠D=360°．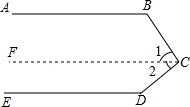

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

    （1）求证：OE=OF；
    （2）若CE=12，CF=5，求OC的长；
    （3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在平行四边形ABCD中，AD＞AB．

    （1）作出∠ABC的平分线（尺规作图，保留作图痕迹，不写作法）；
    （2）若（1）中所作的角平分线交AD于点E，AF⊥BE，垂足为点O，交BC于点F，连接EF．求证：四边形ABFE为菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为，则的值为

    A．16 B．17 C．18 D．19

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知a∥b，小亮把三角板的直角顶点放在直线b上，若∠1＝40°，则∠2的度数为________．

    查看答案和解析>>

    同步练习册答案