
【题目】如图,二次函数![]() 图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为
图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为![]() 、3,与y轴负半轴交于点C,在下面四个结论中:
、3,与y轴负半轴交于点C,在下面四个结论中:
①![]() ;②
;②![]() ;
;![]() 只有当
只有当![]() 时,
时,![]() 是等腰直角三角形;其中正确的结论是__________
是等腰直角三角形;其中正确的结论是__________![]() 请把正确结论的序号都填上
请把正确结论的序号都填上![]()

【答案】①②③
【解析】分析:先根据图象与x轴的交点A,B的横坐标分别为1,3,确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
详解:①∵图象与x轴的交点A,B的横坐标分别为1,3,
∴AB=4,
∴对称轴![]()
即2a+b=0.故①正确;
②∵A点坐标为(1,0),
∴ab+c=0,而b=2a,
∴a+2a+c=0,即c=3a.故②正确;
③要使△ABD为等腰直角三角形,必须保证D到x轴的距离等于AB长的一半;
D到x轴的距离就是当x=1时y的值的绝对值。
当x=1时,y=a+b+c,
即|a+b+c|=2,
∵当x=1时y<0,
∴a+b+c=2,
又∵图象与x轴的交点A,B的横坐标分别为1,3,
∴当x=1时y=0,即ab+c=0,
x=3时y=0,即9a+3b+c=0,
解这三个方程可得:![]() 故③正确;
故③正确;
故答案为:①②③.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q分别为AB、BC边上的动点,点P从点A开始沿AB方向运动,且速度为每秒1cm,点Q从点B开始B→C方向运动,且速度为每秒2cm,它们同时出发;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形?
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分?若能够,请求出运动时间;若不能够,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.
(提出问题)三个有理数a,b,c,满足![]() ,求
,求![]() 的值.
的值.
(解决问题).
解:由题意得,a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即![]() ,
,![]() ,
,![]() 时,则
时,则![]() (备注:一个非零数除以它本身等于1,如
(备注:一个非零数除以它本身等于1,如![]() ,则
,则![]() ,
,![]() )
)
②当a,b,c有一个为正数,另两个为负数时,设![]() ,
,![]() ,
,![]() ,
,
则![]() .
.
(备注:一个非零数除以它的相反数等于-1,如:![]() ,则
,则![]() ).
).
所以![]() 的值为3或一1.
的值为3或一1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的虚线网格我们称为正三角形网格,它的每一个小三角形都是边长为 1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)图①中,已知四边形 ABCD 是平行四边形,求△ABC 的面积和对角线 AC 的长;
(2)图②中,求四边形 EFGH 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划投入50万元,开发并生产甲乙两种产品,根据市场调查预计甲产品的年获利y1(万元)与投入资金x(万元)成正比例,乙产品的年获利y2(万元)与投入资金x(万元)的平方成正比例,设该公司投入乙产品x(万元),两种产品的年总获利为y万元(x≥0),得到了表中的数据.
x(万元) | 20 | 30 |
y(万元) | 10 | 13 |
(1)求y与x的函数关系式;
(2)该公司至少可获得多少利润?请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议,使他能获得最大利润,并求出最大利润是多少?
(3)若从年总利润扣除投入乙产品资金的a倍(a≤1)后,剩余利润随x增大而减小,求a的取值
范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).请解答下列问题:
(1)如果购买乒乓球![]() (
(![]() 不小于5)盒,则在甲店购买需付款 元,在乙店购买需付款 元。(用
不小于5)盒,则在甲店购买需付款 元,在乙店购买需付款 元。(用![]() 的代数式表示)
的代数式表示)
(2)当购买乒乓球多少盒时,在两店购买付款一样?
(3)如果给你450元,让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读资料,解决问题.
人教版《数学九年级(下册)》的![]() 页有这样一个思考问题:
页有这样一个思考问题:
问题:如图,在![]() 中,
中,![]() 交
交![]() ,
,![]() 于点
于点![]() ,
,![]() ,如果通过“相似的定义”证明
,如果通过“相似的定义”证明![]() ?
?
根据“两直线平行,同位角相等”容易得出三对对应角分别相等,再根据“平行线分线段成比例”的基本事实,容易得出![]() ,所以这个问题的核心时如何证明“
,所以这个问题的核心时如何证明“![]() ”.
”.
证明思路:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,构造平行四边形
,构造平行四边形![]() ,得到
,得到![]() ,从而将比例式中的
,从而将比例式中的![]() ,
,![]() 转化为共线的两条线段
转化为共线的两条线段![]() ,
,![]() ,同时也构造了基本图形“
,同时也构造了基本图形“ ”,得到
”,得到![]() ,从而得证.
,从而得证.

解决问题:
(![]() )①类比资料中的证明思路,请你证明“三角形内角平分线定理”.
)①类比资料中的证明思路,请你证明“三角形内角平分线定理”.
三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
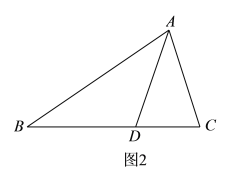
已知:如图![]() ,
,![]() 中,
中,![]() 是角平分线.
是角平分线.
求证:![]() .
.

②运用“三角形内角平分线定理”填空:
已知:如图![]() ,
,![]() 中,
中,![]() 是角平分线,
是角平分线,![]() ,
,![]() ,
,![]() ,则
,则![]() __________.
__________.
(![]() )我们知道,如果两个三角形有相同的高或者相等的高,那么它们面积的比就等于底的比.
)我们知道,如果两个三角形有相同的高或者相等的高,那么它们面积的比就等于底的比.
请你通过研究![]() 和
和![]() 面积的比来证明三角形内角平分线定理.
面积的比来证明三角形内角平分线定理.
已知:如图![]() ,
,![]() 中,
中,![]() 是角平分线.
是角平分线.
求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com