
【题目】在平面直角坐标系中,点A,B为反比例函数y=![]() (k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
(k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
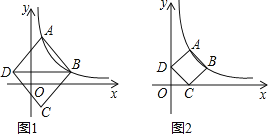
(1)如图1,点A,B横坐标分别为1,4,对角线BD∥x轴,菱形ABCD面积为![]() ,求k的值.
,求k的值.
(2)如图2,当点A,B运动至某一时刻,点C,点D恰好落在x轴和y轴正半轴上,此时∠ABC=90°,求点A,B的坐标.
【答案】(1)![]() ;(2)A(
;(2)A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() )
)
【解析】
(1)由菱形的性质可得BD=2BE=6,AC⊥DB,由菱形的面积公式可求AC=![]() ,设点B(4,a),则点A(1,
,设点B(4,a),则点A(1,![]() +a),代入解析式可求a的值,从而求出k的值;
+a),代入解析式可求a的值,从而求出k的值;
(2)过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,设点A(m,![]() )由全等三角形的性质可得AE=DO=CF=m,DE=OC=BF=
)由全等三角形的性质可得AE=DO=CF=m,DE=OC=BF=![]() ﹣m,可表示B坐标,代入解析式可求解.
﹣m,可表示B坐标,代入解析式可求解.
解:(1)连接AC,交BD于点E,

∵点A,B横坐标分别为1,4,对角线BD∥x轴,
∴BE=4﹣1=3,
∵四边形ABCD是菱形,
∴BD=2BE=6,AC⊥DB,
∵菱形ABCD面积为![]() ,
,
∴![]() ×BD×AC=
×BD×AC=![]() ,
,
∴AC=![]() ,
,
∴AE=CE=![]() ,
,
设点B(4,a),则点A(1,![]() +a),
+a),
∵点A,B为反比例函数y=![]() (k>0,x>0)上的两个点,
(k>0,x>0)上的两个点,
∴4a=1×(![]() +a),
+a),
∴a=![]() ,
,
∴k=4a=![]() ;
;
(2)如图,过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,

∵四边形ABCD是菱形,∠ABC=90°,
∴四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠DCB=90°,
∴∠ADE+∠EAD=90°,∠EDA+∠CDO=90°,∠DCO+∠CDO=90°,∠BCF+∠DCO=90°,
∴∠EAD=∠CDO=∠BCF,且∠AED=∠DOC=90°,AD=CD,
∴△AED≌△DOC(AAS),
∴AE=DO,ED=OC,
同理可得:BF=OC,CF=DO,
设点A(m,![]() ),
),
∴AE=DO=CF=m,DE=OC=BF=![]() ﹣m,
﹣m,
∴点B坐标(![]() ,
,![]() ﹣m),
﹣m),
∴![]() (
(![]() ﹣m)=
﹣m)=![]() ,
,
∴m1=![]() ,m2=﹣
,m2=﹣![]() (舍去),
(舍去),
∴点A(![]() ,
,![]() ),点B(
),点B(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
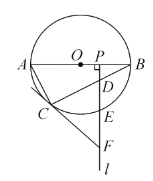
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小红将这五位名人简介分别写在五张完全相同的知识卡片上.
(1)小哲从中随机抽取一张,求卡片上介绍的人物是唐太宗的概率;
(2)用树状图或列表法求小哲从中随机抽取两张,卡片上介绍的人物均是汉朝以后出生的概率.(注:唐太宗、宋太祖、成吉思汗均是汉朝以后出生)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC为等腰直角三角形,AB=AC,△ADE为等腰直角三角形,AD=AE,点D在直线BC上,连接CE.
(1)判断:①CE、CD、BC之间的数量关系;②CE与BC所在直线之间的位置关系,并说明理由;
(2)若D在CB延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请说明理由;
(3)若D在BC延长线上,(1)中的结论是否成立?若成立,请直接写出结论,若不成立,请写出你发现的结论,并计算:当CE=10cm,CD=2cm时,BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)若由甲挑一名选手打第一场比赛,选中乙的概率是 ;
(2)任选两名同学打第一场,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (x>0)的图象与直线
(x>0)的图象与直线![]() 相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.
相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com