
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y=ax2+bx+c | … | t | m | -2 | -2 | n | … |
根据以上列表,回答下列问题:
(1)直接写出c的值和该二次函数图象的对称轴;
(2)写出关于x的一元二次方程ax2+bx+c=t的根;
(3)若m=-1,求此二次函数的解析式.
科目:初中数学 来源: 题型:
【题目】为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
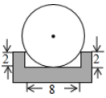
A.12 cmB.10 cmC.8 cmD.6 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=3,BC=4,O是BC的中点,到点O的距离等于![]() BC的所有点组成的图形记为G,图形G与AB交于点D.
BC的所有点组成的图形记为G,图形G与AB交于点D.

(1)补全图形并求线段AD的长;
(2)点E是线段AC上的一点,当点E在什么位置时,直线ED与 图形G有且只有一个交点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠B=60°,AB=3cm,过点A作∠EAF=60°,分别交DC,BC的延长线于点E,F,连接EF.
(1)如图1,当CE=CF时,判断△AEF的形状,并说明理由;
(2)若△AEF是直角三角形,求CE,CF的长度;
(3)当CE,CF的长度发生变化时,△CEF的面积是否会发生变化,请说明理由.
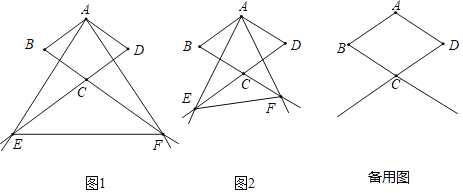
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公司要建一个矩形的产品展示台,展示台的一边靠找为9m的宣传版(这条边不能超出宣传版),另三边用总长为40m的红布粘贴在展示台边上.设垂直于宣传版的一边长为![]()
(1)当展示台的面积为128m2时,求![]() 的值;
的值;
(2)设展示台的面积为![]() ,求
,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=![]() ,请你解答下列问题:
,请你解答下列问题:
(1)m= ,抛物线与x轴的交点为 .
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y<0?
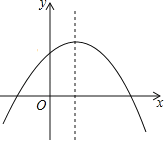
查看答案和解析>>
科目:初中数学 来源: 题型:
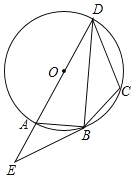
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com