
【题目】已知AB为⊙O的直径,CD为⊙O的弦,CD∥AB,过点B的切线与射线AD交于点M,连接AC,BD.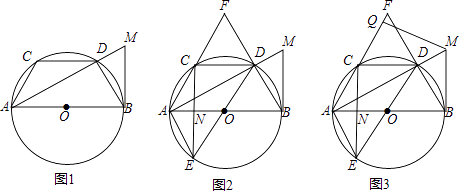
(1)如图l,求证:AC=BD;
(2)如图2,延长AC、BD交于点F,作直径DE,连接AE、CE,CE与AB交于点N,求证:∠AFB=2∠AEN;
(3)如图3,在(2)的条件下,过点M作MQ⊥AF于点Q,若MQ:QC=3:2,NE=2,求QF的长.
【答案】
(1)证明:连接OC,OD,
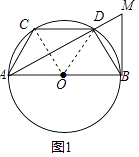
∵CD∥AB,
∴∠DAB=∠ADC,
∵∠DOB=2∠DAB,∠COA=2∠CDA,
∴∠COA=∠DOB,
∴AC=BD;
(2)连接OC,
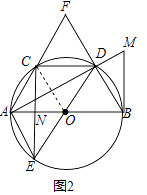
∵∠COA=∠DOB,OA=OB=OC=OD,
∴∠CAB=∠DBA,
∴△FBA是等腰三角形,
∵DE是⊙O的直径,
∴∠ECD=90°,
∵CD∥AB,
∴∠ANC=90°,
∴AB⊥CE,
∴AC=AE,
∴∠CAN=∠EAN=∠ABF,∠ACE=∠AEN,
∵∠FAB+∠FBA+∠F=180°,∠CAE+∠AEC+∠ACE=180°,
∴∠F=∠ACE+∠AEC,
∴∠AFB=2∠AEN;
(3)解:连接BC交AD于P,
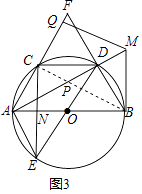
∵AC=BD,
∴ ![]() =
= ![]() ,
,
∴∠PAB=∠PBA,
∴PA=PB,∠PBM=∠PMB,
∴PB=PM,
∴P为AM的中点,
∵MQ⊥AF,BC⊥AF,
∴BC∥MQ,
∴ ![]() =
= ![]() ,
,
∴AC=CQ,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴tan∠MAQ= ![]() ,
,
∴tan∠F= ![]() ,
,
设DF=3k,AD=4k,由勾股定理得,AF=5k=BF,
∴BD=2k,
∴tan∠ABD=2,
∴DE为直径,
∴∠EAD=90=∠BDM,
∴AE∥BD,
∴∠EAN=∠ABD,
∴tan∠EAN=2,
∵NE=2,
∴AN=1,CN=2,
∴BN=4,AE=BD= ![]() ,
,
∴DF= ![]() ,AC=BD=
,AC=BD= ![]() =CQ,
=CQ,
∴QF= ![]()
【解析】(1)由平行线的内错角相等性质、圆周角定理可推出AC=BD;(2)由于∠AEN是圆周角,因此2∠AEN可转化为圆心角∠COA,问题转化为证∠COA=∠AFB,两个角都是等腰三角形的顶角,转化为证底角相等,即∠CAN=∠EAN=∠ABF,由垂径定理推论易证出结论;(3)利用圆周角定理的推论可推出tan∠MAQ= ![]() ,进而推出tan∠F=
,进而推出tan∠F= ![]() ,设出参数,求出AC,进而求出AQ,用AF减去AQ可求出QF
,设出参数,求出AC,进而求出AQ,用AF减去AQ可求出QF


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: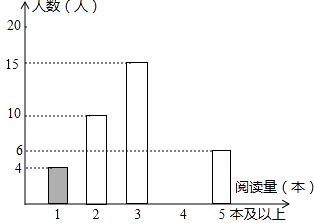
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
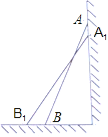
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=![]()
而A1B1=2.5,在Rt△A1B1C中,由![]() 得方程 ,
得方程 ,
解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
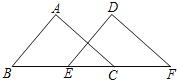
(1)当△ABC所扫过的面积为32时,求a的值;
(2)连接AE、AD,当AB=5,a=5时,试判断△ADE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计,并绘制如图所示的扇形统计图和条形统计图.根据图中信息解答下列问题:
(1)该超市“元旦”期间共销售 个绿色鸡蛋,A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度;
(2)补全条形统计图;
(3)如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个,请你估计这个分店销售的B种品牌的绿色鸡蛋的个数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣3|+(﹣1)2016×(π﹣3.14)0﹣(![]() )﹣2+2﹣3
)﹣2+2﹣3
(2)利用乘法公式计算:20182﹣2017×2019
(3)已知2a=3,4b=5,8c=7,求8a+c﹣2b的值.
(4)已知x2﹣5x=14,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正比例函数y=ax的图象与反比例函数y= ![]() 的图象交于点C(3,1)
的图象交于点C(3,1)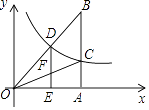
(1)试确定上述比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com