
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻߵĶ„µćDµÄ×ų±źĪŖ£Ø©1£¬4£©£¬Å×ĪļĻßÓėxÖįĻą½»ÓŚA£®BĮ½µć£ØAŌŚBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£Ø0£¬3£©£®
£Ø1£©ĒóÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©ČēĶ¼1£¬ŅŃÖŖµćE£Ø0£¬©3£©£¬ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚŅ»µćF£¬Ź¹µĆ”÷CEFµÄÖܳ¤×īŠ”£¬Čē¹ū“ęŌŚ£¬Ēó³öµćFµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©ČēĶ¼2£¬Į¬½ÓAD£¬ČōµćPŹĒĻ߶ĪOCÉĻµÄŅ»¶Æµć£¬¹żµćP×÷Ļ߶ĪADµÄ“¹Ļߣ¬ŌŚµŚ¶žĻóĻŽ·Ö±šÓėÅ×ĪļĻß”¢Ļ߶ĪADĻą½»ÓŚµćM”¢N£¬µ±MN×ī“óŹ±£¬Ēó”÷POMµÄĆ껿£®
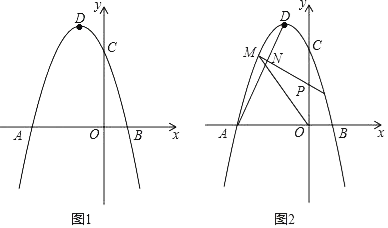
”¾“š°ø”æ(1)y=©x2©2x+3£»(2) “ęŌŚ, F£Ø©1£¬0£©,ĄķÓɼū½āĪö£»£Ø3£©2
”¾½āĪö”æ
(1)øł¾Ż¶„µćŹ½æÉĒóµĆÅ×ĪļĻߵıķ“ļŹ½;
(2) ČēĶ¼ 1£¬×÷ C¹ŲÓŚ¶Ō³ĘÖįµÄ¶Ō³Ęµć C”䣬Į¬½ÓEC”ä½»¶Ō³ĘÖįÓŚ F£¬øł¾ŻÖį¶Ō³ĘµÄ×ī¶ĢĀ·¾¶ĪŹĢā, CF+EFµÄÖµ×īŠ”£¬Ōņ”÷CEFµÄÖܳ¤×īŠ”;
(3)ČēĶ¼2,ĻČĄūÓĆ“ż¶ØĻµŹż·ØĒóADµÄ½āĪöŹ½ĪŖ: y£½2x+6,ÉčM£Øm£¬©m2©2m+3£©£¬ŌņG£Øm£¬2m+6£©£¬£Ø©3”Üm”Ü©1£©,Ö¤Ć÷”÷MNG”×”÷AHD,ĮŠ±ČĄżŹ½æɵĆMNµÄ±ķ“ļŹ½,øł¾ŻÅä·½·ØæɵƵ±m=-2Ź±,MNÓŠ×ī“óÖµ,Ö¤Ć÷”÷MCP”×”÷DHA,Ķ¬ĄķµĆPCµÄ³¤,“Ó¶ųµĆOPµÄ³¤,øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½æÉµĆ½įĀŪ,²¢½«m=-2“śČė¼ĘĖć¼“æÉ
£Ø1£©ÉčÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗy£½a£Øx+1£©2+4£¬
°Ńx£½0£¬y£½3“śČėµĆ£ŗ3£½a£Ø0+1£©2+4£¬½āµĆ£ŗa£½©1
”ąÅ×ĪļĻߵıķ“ļŹ½ĪŖy£½©£Øx+1£©2+4£½©x2©2x+3£»
£Ø2£©“ęŌŚ£®ČēĶ¼ 1£¬×÷ C¹ŲÓŚ¶Ō³ĘÖįµÄ¶Ō³Ęµć C”䣬Į¬½ÓEC”ä½»¶Ō³ĘÖįÓŚ F£¬“ĖŹ± CF+EFµÄÖµ×īŠ”£¬Ōņ”÷CEFµÄÖܳ¤×īŠ”£®
”ßC£Ø0£¬3£©£¬
”ąC”ä£Ø©2£¬3£©£¬Ņ×µĆC”äEµÄ½āĪöŹ½ĪŖ£ŗy£½©3x©3£¬
µ±x£½©1Ź±£¬y£½©3”Į£Ø©1£©©3£½0£¬
”ąF£Ø©1£¬0£©
£Ø3£©ČēĶ¼2£¬”ßA£Ø©3£¬0£©£¬D£Ø©1£¬4£©£¬
Ņ×µĆADµÄ½āĪöŹ½ĪŖ£ŗy£½2x+6£¬
¹żµćD×÷DH”ĶxÖįÓŚH£¬¹żµćM×÷MG”ĶxÖį½»ADÓŚG£¬
AH£½©1©£Ø©3£©£½2£¬DH£½4£¬”ąAD£½![]() £¬
£¬
ÉčM£Øm£¬©m2©2m+3£©£¬ŌņG£Øm£¬2m+6£©£¬£Ø©3”Üm”Ü©1£©£¬
”ąMG£½£Ø©m2©2m+3£©©£Ø2m+6£©£½©m2©4m©3£¬
ÓÉĢāŅ×ÖŖ”÷MNG”×”÷AHD£¬
”ą![]()
¼“![]()
ӧ![]()
”ąµ±m£½©2Ź±£¬MNÓŠ×ī“óÖµ£»
“ĖŹ±M£Ø©2£¬3£©£¬ÓÖ”ßC£Ø0£¬3£©£¬Į¬½ÓMC
”ąMC”ĶyÖį
”ß”ĻCPM£½”ĻHAD£¬”ĻMCP£½”ĻDHA£½90”ć£¬
”ą”÷MCP”×”÷DHA£¬
”ą![]()
¼“ ![]()
”ąPC£½1
”ąOP£½OC©PG£½3©1£½2£¬
”ąS”÷POM£½![]() £½2£¬
£½2£¬



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ ČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻC=90”ć£¬µćOŌŚ±ßBCÉĻ£¬ŅŌµćOĪŖŌ²ŠÄ£¬OBĪŖ°ė¾¶µÄŌ²¾¹żµćA£¬¹żµćA×÷Ö±ĻßAD£¬Ź¹”ĻCAD=2”ĻB£®

£Ø1£©ÅŠ¶ĻÖ±ĻßADÓė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ČōOB=4£¬”ĻCAD=60”ć£¬ĒėÖ±½ÓŠ“³öĶ¼ÖŠĻŅABÓė![]() Ī§³ÉµÄŅõÓ°²æ·ÖµÄĆ껿£®
Ī§³ÉµÄŅõÓ°²æ·ÖµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ ČēĶ¼1£¬ŅŃÖŖĖ®ĮśĶ·ÅēĖ®µÄ³õŹ¼ĖŁ¶Čv0æÉŅŌ·Ö½āĪŖŗįĻņ³õŹ¼ĖŁ¶ČvxŗĶׯĻņ³õŹ¼ĖŁ¶Čvy£¬¦ČŹĒĖ®ĮśĶ·µÄŃö½Ē£¬ĒŅv02=vx2+vy2£®Ķ¼2ŹĒŅ»øö½ØŌŚŠ±ĘĀÉĻµÄ»ØĘŌ³”µŲµÄ½ŲĆęŹ¾ŅāĶ¼£¬Ė®ĮśĶ·µÄÅēÉäµćAŌŚÉ½ĘĀµÄĘĀ¶„ÉĻ£ØÅēÉäµćĄėµŲĆęø߶ČŗöĀŌ²»¼Ę£©£¬ĘĀ¶„µÄĒ¦Ö±ø߶ČOAĪŖ15Ć×£¬É½ĘĀµÄĘĀ±ČĪŖ![]() £®ĄėæŖĖ®ĮśĶ·ŗóµÄĖ®£Øæ“³Éµć£©»ńµĆ³õŹ¼ĖŁ¶Čv0Ć×/ĆėŗóµÄŌĖ¶ÆĀ·¾¶æÉŅŌæ“×÷ŹĒÅ×ĪļĻߣ¬µćMŹĒŌĖ¶Æ¹ż³ĢÖŠµÄijŅ»Ī»ÖĆ£®ŗöĀŌæÕĘų×čĮ¦£¬ŹµŃé±ķĆ÷£ŗMÓėAµÄø߶ČÖ®²īd£ØĆ×£©ÓėÅē³öŹ±¼ät£ØĆė£©µÄ¹ŲĻµĪŖd=vyt-5t2£»MÓėAµÄĖ®Ę½¾ąĄėĪŖvxtĆ×£®ŅŃÖŖøĆĖ®Į÷µÄ³õŹ¼ĖŁ¶Čv0ĪŖ15Ć×/Ćė£¬Ė®ĮśĶ·µÄŃö½Ē¦ČĪŖ53”ć£®
£®ĄėæŖĖ®ĮśĶ·ŗóµÄĖ®£Øæ“³Éµć£©»ńµĆ³õŹ¼ĖŁ¶Čv0Ć×/ĆėŗóµÄŌĖ¶ÆĀ·¾¶æÉŅŌæ“×÷ŹĒÅ×ĪļĻߣ¬µćMŹĒŌĖ¶Æ¹ż³ĢÖŠµÄijŅ»Ī»ÖĆ£®ŗöĀŌæÕĘų×čĮ¦£¬ŹµŃé±ķĆ÷£ŗMÓėAµÄø߶ČÖ®²īd£ØĆ×£©ÓėÅē³öŹ±¼ät£ØĆė£©µÄ¹ŲĻµĪŖd=vyt-5t2£»MÓėAµÄĖ®Ę½¾ąĄėĪŖvxtĆ×£®ŅŃÖŖøĆĖ®Į÷µÄ³õŹ¼ĖŁ¶Čv0ĪŖ15Ć×/Ćė£¬Ė®ĮśĶ·µÄŃö½Ē¦ČĪŖ53”ć£®

£Ø1£©ĒóĖ®Į÷µÄŗįĻņ³õŹ¼ĖŁ¶ČvxŗĶׯĻņ³õŹ¼ĖŁ¶Čvy£»
£Ø2£©ÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾µćMµÄŗį×ų±źxŗĶׯ×ų±źy£¬²¢ĒóyÓėxµÄ¹ŲĻµŹ½£Ø²»Š“xµÄȔֵ·¶Ī§£©£»
£Ø3£©Ė®Į÷ŌŚÉ½ĘĀÉĻµÄĀäµćCĄėÅēÉäµćAµÄĖ®Ę½¾ąĄėŹĒ¶ąÉŁĆ×£æČōŅŖŹ¹Ė®Į÷Ē”ŗĆÅēÉäµ½ĘĀ½ÅB“¦µÄŠ”Ź÷£¬ŌŚĻąĶ¬Ńö½ĒĻĀ£¬ŌņŠčŅŖ°ŃÅēÉäµćAŃŲĘĀĆęAB·½ĻņŅĘ¶Æ¶ąÉŁĆ×£æ£Ø²Īæ¼Źż¾Ż£ŗsin53”ć”Ö![]() £¬cos53”ć”Ö
£¬cos53”ć”Ö![]() £¬tan53”ć”Ö
£¬tan53”ć”Ö![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
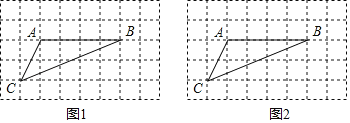
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ8”Į5µÄÕż·½ŠĪĶųøńÖŠ£¬ĆæøöŠ”Õż·½ŠĪµÄ±ß³¤¾łĪŖ1£¬”÷ABCµÄČżøö¶„µć¾łŌŚŠ”Õż·½ŠĪµÄ¶„µćÉĻ£®
£Ø1£©ŌŚĶ¼1ÖŠ»³ö”÷ABD£ØµćDŌŚŠ”Õż·½ŠĪµÄ¶„µćÉĻ£©£¬Ź¹”÷ABDµÄÖܳ¤µČÓŚ”÷ABCµÄÖܳ¤£¬ĒŅĖıߊĪACBDŹĒÖŠŠÄ¶Ō³ĘĶ¼ŠĪ£»
£Ø2£©ŌŚĶ¼2ÖŠÕŅŅ»µćE£ØµćEŌŚŠ”Õż·½ŠĪµÄ¶„µćÉĻ£©£¬Ź¹tan”ĻAEB£½2£ØAE£¼EB£©£¬ĒŅĖıߊĪACEBµÄ¶Ō±ß²»Ę½ŠŠ£¬²¢Ö±½ÓŠ“³öĶ¼2ÖŠĖıߊĪACEBµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
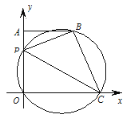
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬A(0£¬4)£¬B(3£¬4)£¬P ĪŖĻ߶Ī OA ÉĻŅ»¶Æµć£¬¹ż O£¬P£¬B ČżµćµÄŌ²½» x ÖįÕż°ėÖįÓŚµć C£¬Į¬½į AB, PC£¬BC£¬Éč OP=m.
£Ø1£©ĒóÖ¤£ŗµ± P Óė A ÖŲŗĻŹ±£¬ĖıߊĪ POCB ŹĒ¾ŲŠĪ.
£Ø2£©Į¬½į PB£¬Ēó tan”ĻBPC µÄÖµ.
£Ø3£©¼ĒøĆŌ²µÄŌ²ŠÄĪŖ M£¬Į¬½į OM£¬BM£¬µ±ĖıߊĪ POMB ÖŠÓŠŅ»×é¶Ō±ßĘ½ŠŠŹ±£¬ĒóĖłÓŠĀś×ćĢõ¼žµÄ m µÄÖµ.
£Ø4£©×÷µć O ¹ŲÓŚ PC µÄ¶Ō³ĘµćO £¬ŌŚµć P µÄÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬µ±µćO ĀäŌŚ”÷APB µÄÄŚ²æ (ŗ¬±ß½ē)Ź±£¬ĒėŠ“³ö m µÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°2018Ī÷°²¹ś¼ŹĀķĄĖÉ”±ÓŚ2018Äź10ŌĀ20ČÕŌŚÉĀĪ÷Ī÷°²¾ŁŠŠ£¬øĆČüŹĀ¹²ÓŠČżĻī£ŗ![]() £®”°ĀķĄĖÉ”±”¢
£®”°ĀķĄĖÉ”±”¢![]() £®”°°ė³ĢĀķĄĖÉ”±”¢
£®”°°ė³ĢĀķĄĖÉ”±”¢![]() £®”°ĆŌÄćĀķĄĖÉ”±Š”Ć÷ŗĶŠ”øÕÓŠŠŅ²ĪÓėĮĖøĆĻīČüŹĀµÄÖ¾ŌøÕß·žĪń¹¤×÷£¬×éĪÆ»įĖ껜½«Ö¾ŌøÕß·ÖÅäµ½ČżøöĻīÄæ×飮
£®”°ĆŌÄćĀķĄĖÉ”±Š”Ć÷ŗĶŠ”øÕÓŠŠŅ²ĪÓėĮĖøĆĻīČüŹĀµÄÖ¾ŌøÕß·žĪń¹¤×÷£¬×éĪÆ»įĖ껜½«Ö¾ŌøÕß·ÖÅäµ½ČżøöĻīÄæ×飮
£Ø1£©Š”Ć÷±»·ÖÅäµ½”°ĆŌÄćĀķĄĖÉ”±ĻīÄæ×éµÄøÅĀŹĪŖ________£®
£Ø2£©ĄūÓĆĮŠ±ķ»ņŹ÷דĶ¼ĒóŠ”Ć÷ŗĶŠ”øÕ±»·ÖÅäµ½²»Ķ¬ĻīÄæ×éµÄøÅĀŹ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔·åŗĶŠ”ŠłÓĆĮ½Ć¶ÖŹµŲ¾łŌȵÄ÷»×Ó×öÓĪĻ·£¬¹ęŌņČēĻĀ£ŗĆæČĖĖ껜֥Į½Ć¶÷»×ÓŅ»“Ī£ØČōÖĄ³öµÄĮ½Ć¶÷»×ÓŽūŌŚŅ»Ęš£¬ŌņÖŲÖĄ£©£¬µćŹżŗĶ“óµÄ»ńŹ¤£»µćŹżŗĶĻąĶ¬ĪŖĘ½¾Ö£®
ŅĄ¾ŻÉĻŹö¹ęŌņ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ė껜֥Į½Ć¶÷»×ÓŅ»“Ī£¬ÓĆĮŠ±ķ·Ø»ņŹ÷דĶ¼·ØĒóµćŹżŗĶĪŖ10µÄøÅĀŹ£»
£Ø2£©Š”·åĻČĖ껜֥Į½Ć¶÷»×ÓŅ»“Ī£¬µćŹżŗĶŹĒ10£¬Ē󊔊łĖ껜֥Į½Ć¶÷»×ÓŅ»“Ī£¬Ź¤Š”·åµÄøÅĀŹ£®£Ø÷»×Ó£ŗĮłøöĆę·Ö±šÓŠ1”¢2”¢3”¢4”¢5”¢6øöŠ”Ō²µćµÄĮ¢·½æ飮µćŹżŗĶ£ŗĮ½Ć¶÷»×Ó³ÆÉĻµÄµćŹżÖ®ŗĶ£®£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×æŚ“ü֊װӊĮ½øöĻąĶ¬µÄŠ”Ēņ£¬ĖüĆĒ·Ö±šŠ“ÓŠ1ŗĶ2£»ŅŅæŚ“ü֊װӊȿøöĻąĶ¬µÄŠ”Ēņ£¬ĖüĆĒ·Ö±šŠ“ÓŠ3”¢4ŗĶ5£»±ūæŚ“ü֊װӊĮ½øöĻąĶ¬µÄŠ”Ēņ£¬ĖüĆĒ·Ö±šŠ“ÓŠ6ŗĶ7£®“ÓÕā3øöæŚ“üÖŠø÷Ė껜µŲČ”³ö1øöŠ”Ēņ£®
(1)Č”³öµÄ3øöŠ”ĒņÉĻĒ”ŗĆÓŠĮ½øöżŹżµÄøÅĀŹŹĒ¶ąÉŁ£æ
(2)Č”³öµÄ3øöŠ”ĒņÉĻČ«ŹĒĘꏿµÄøÅĀŹŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÄŚ½ÓÓŚŅŌABĪŖÖ±¾¶µÄ”ŃO£¬¹żµćA×÷”ŃOµÄĒŠĻߣ¬ÓėBCµÄŃÓ³¤ĻßĻą½»ÓŚµćD£¬ŌŚCBÉĻ½ŲČ”CE£½CD£¬Į¬½ÓAE²¢ŃÓ³¤£¬½»”ŃOÓŚµćF£¬Į¬½ÓCF£®
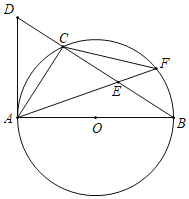
£Ø1£©ĒóÖ¤£ŗAC£½CF£»
£Ø2£©ČōAB£½4£¬sinB![]() £¬ĒóEFµÄ³¤£®
£¬ĒóEFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com