
 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,求DE的长.
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,求DE的长.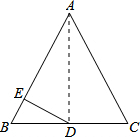 解:连接AD,
解:连接AD,| 1 |
| 2 |
| AB2-BD2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BD•AD |
| AB |
| 5×12 |
| 13 |
| 60 |
| 13 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| A、开口向上,对称轴是y轴 |
| B、开口向下,对称轴是y轴 |
| C、开口向上,对称轴平行于y轴 |
| D、开口向下,对称轴平行于y轴 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、y1>y2 |
| B、y1>y2>0 |
| C、y1<y2 |
| D、y1=y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,反比例函数y=
如图,反比例函数y=| -8 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
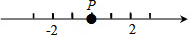 某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点P在数轴上做直线运动的一个雏形,如图所示.点P从原点开始运动至停止的记录为:+12,-8,-2,-7,+3.问:当运动停止时,点P位置上的数是多少?
某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点P在数轴上做直线运动的一个雏形,如图所示.点P从原点开始运动至停止的记录为:+12,-8,-2,-7,+3.问:当运动停止时,点P位置上的数是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
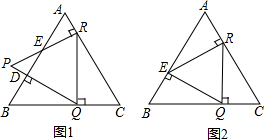 如图1,D是边长为8cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P.
如图1,D是边长为8cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com