
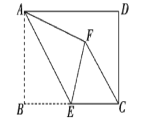
【题目】如图,四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,连接
是等边三角形,连接![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
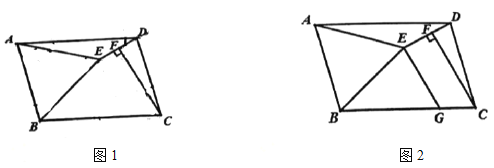
【答案】(1)30°;(2)证明见详解.
【解析】
(1)由四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,得∠BAE=60°,∠BAD+∠ADC=180°,从而得∠DAE+∠ADE+∠CDF=120°,结合
是等边三角形,得∠BAE=60°,∠BAD+∠ADC=180°,从而得∠DAE+∠ADE+∠CDF=120°,结合![]() ,
,![]() ,即可求解;
,即可求解;
(2)连接CE,在线段BG上截取BM=GC,易证CFECFD(SAS),得CD=CE,∠DCF=∠ECF,再证MBEGCE(SAS),得ME=GE,由∠ABE=60°,∠ABC+∠BCD=180°,得∠MBE+∠GCE+∠DCF+∠ECF=120°,从而得∠FCB=60°,易证CF∥GE,得∠EGM=∠FCB=60°,EMG是等边三角形,进而得GE=GM,即可得到结论.
(1)∵四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,
是等边三角形,
∴∠BAE=60°,∠BAD+∠ADC=180°,
∴∠DAE+∠ADE+∠CDF=180°-∠BAE=180°-60°=120°,
∵![]() ,
,
∴∠DCF+∠ADE+∠CDF=120°,
∵![]() ,
,
∴∠DCF+∠CDF=90°,
∴∠ADE=120°-(∠DCF+∠CDF)= 120°-90°=30°;
(2)连接CE,在线段BG上截取BM=GC,
∵![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
∴∠CFE=∠CFD=90°,EF=DF,
∵CF=CF,
∴CFECFD(SAS),
∴CD=CE,∠DCF=∠ECF,
∵四边形![]() 是平行四边形,
是平行四边形,![]() 是等边三角形,
是等边三角形,
∴CD=AB=BE,
∴CE=BE,
∴∠MBE=∠GCE,
在MBE和GCE中,
∵ ,
,
∴ MBEGCE(SAS),
∴ME=GE,
∵∠ABE=60°,∠ABC+∠BCD=180°,
∴∠MBE+∠BCD=180°-∠ABE=180°-60°=120°,
即:∠MBE+∠GCE+∠DCF+∠ECF=120°,
∴∠GCE+∠ECF=![]() ×120°=60°,即:∠FCB=60°,
×120°=60°,即:∠FCB=60°,
∵![]() ,
,
∴CF∥GE,
∴∠EGM=∠FCB=60°,
∴EMG是等边三角形,
∴GE=GM,
∴BG=GM+BM=GC+GE,即:![]() .
.



科目:初中数学 来源: 题型:
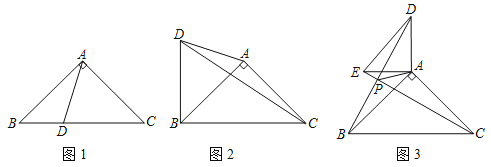
【题目】在△ABC中,AB=AC,∠BAC=90°,D为平面内的一点.
(1)如图1,当点D在边BC上时,且∠BAD=30°,求证:AD=![]() BD.
BD.
(2)如图2,当点D在△ABC的外部,且满足∠BDC﹣∠ADC=45°,求证:BD=![]() AD.
AD.
(3)如图3,若AB=4,当D、E分别为AB、AC的中点,把△DAE绕A点顺时针旋转,设旋转角为α(0<α≤180°),直线BD与CE的交点为P,连接PA,直接写出△PAC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
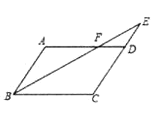
【题目】如图,在口ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= ![]() CD
CD
(1)求证:△ABF∽△CEB
(2)若△DEF的面积为2,求△CEB的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
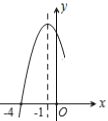
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③一元二次方程
;③一元二次方程![]() 的解是
的解是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】. 某工厂计划生产一批某种产品,数量不超过3500件. 该产品由![]() 三部分组成,分别由厂里甲、乙、丙三个车间完成. 三个车间于某天零时同时开工,每天24小时连续工作. 若干天后的零时,甲车间完成任务;几天后的18时,乙车间完成任务;自乙车间完成任务后的当天零时起,再过几天后的8时,丙车间完成任务. 已知三个车间每天完成
三部分组成,分别由厂里甲、乙、丙三个车间完成. 三个车间于某天零时同时开工,每天24小时连续工作. 若干天后的零时,甲车间完成任务;几天后的18时,乙车间完成任务;自乙车间完成任务后的当天零时起,再过几天后的8时,丙车间完成任务. 已知三个车间每天完成![]() 的数量分别为300件、240件、180件,该工厂完成这种产品的件数是___________.
的数量分别为300件、240件、180件,该工厂完成这种产品的件数是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有![]() 个标号分别为
个标号分别为![]() 的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为
的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为![]() ,再从剩下的
,再从剩下的![]() 个小球中随机取出一个小球,记下标号为
个小球中随机取出一个小球,记下标号为![]() 记点
记点![]() 的坐标为
的坐标为![]() .
.
(1)请用画树形图或列表的方法写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求两次取出的小球标号之和大于![]() 的概率;
的概率;
(3)求点![]() 落在直线
落在直线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠ABC和 ∠BAC的平分线交于点E,延长AE分别交BC, ⊙O于点F, D,连接BD.
(1)求证: BD=DE.
(2)若BD=6,AD=10,求EF的长.
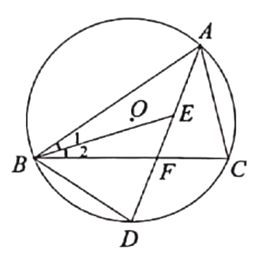
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com