
【题目】如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为点B,AC⊥y轴,垂足为点C.
(1)写出点M的坐标;
(2)求直线MN的表达式;
(3)若点A的横坐标为-1,求矩形ABOC的面积.

【答案】(1)(-2,0);(2)该y=3x+6;(3) S矩形ABOC=3.
【解析】
(1)由点N(0,6),得出ON=6,再由ON=3OM,求得OM=2,得出点M的坐标;
(2)设出直线MN的解析式为:y=kx+b,代入M、N两点求得答案即可;
(3)将A点横坐标代入y=3x+6,求出纵坐标,即可表示出S矩形ABOC.
(1)∵N(0,6)
∴ON=6
∵ON=3OM
∴OM=2
∴M点坐标为(-2,0);
(2)该直线MN的表达式为y=kx+b,分别把M(-2,0),N(0,6)代入,
得 ![]() 解得
解得![]()
∴直线MN的表达式为y=3x+6.
(3)在y=3x+6中,当x=-1时,y=3,∴OB=1,AB=3,
∴S矩形ABOC=1×3=3.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应南充市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等。从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
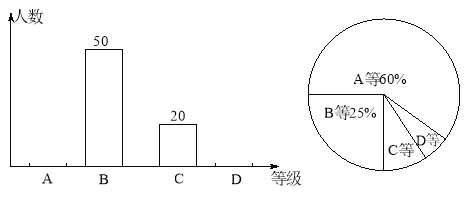
A.样本容量是200
B.D等所在扇形的圆心角为15°
C.样本中C等所占百分比是10%
D.估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数;
(4)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热爱学习的小明同学在网上搜索到下面的文字材料:
在x轴上有两个点它们的坐标分别为![]() 和
和![]() .则这两个点所成的线段的长为
.则这两个点所成的线段的长为![]() ;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b-d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a-c|,P2Q=|b-d|,利用勾股定理可得,线段P1 P2的长为
;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b-d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a-c|,P2Q=|b-d|,利用勾股定理可得,线段P1 P2的长为![]() .
.

根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知![]() ,
,![]() ,则线段AB的长为_____;
,则线段AB的长为_____;
(2)若点C在y轴上,点D的坐标是![]() ,且
,且![]() ,则点C的坐标是_____;
,则点C的坐标是_____;
(3)如图2,在直角坐标系中,点A,B的坐标分别为![]() 和
和![]() ,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
,点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com